Dear Team,
This is a general doubt regarding the transmission line.
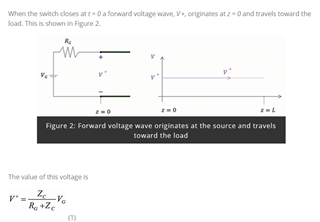
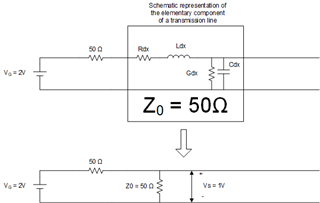
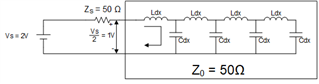
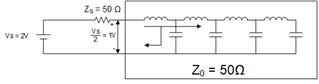
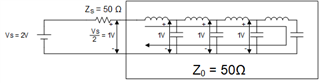
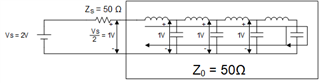
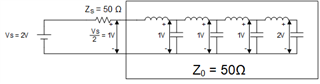
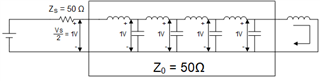
The below figure is an equivalent circuit of an open-ended transmission line. For finding the the voltage at V+ why the author used voltage division.
This is an open-ended transmission line so the voltage at V+ should be the open-circuit voltage Vg?
May I know where I went wrong?
https://incompliancemag.com/article/transmission-line-reflections-at-a-resistive-load/
Regards
HARI