FAQ: Logic and Voltage Translation > Power and Thermals >> Current FAQ
For the short answer - use a 0.1uF for single supply logic devices like the SN74LVC1G08, or a 0.022uF capacitor for each supply pin of a device with multiple supply pins, such as the SN74LVC16244A (which has 4 supply pins).
Why do we need a bypass capacitor at all?
The purpose of a bypass capacitor is to provide a local supply of charge with very low impedance that can be quickly drawn upon by a component for power.
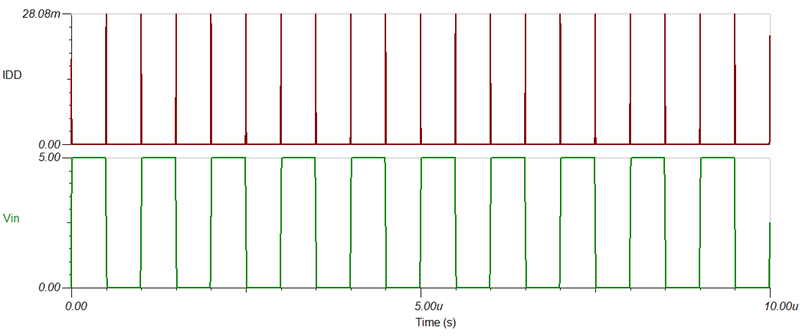
CMOS logic devices require significantly more power to be drawn during switching events than they do while in static operation, which means they must draw power quickly from the supply. Here's a plot of the expected current from a simple CMOS inverter during input switching events (simulated):
As you can see, there are short and sharp power spikes on each input transition. Because these current spikes are very short in duration and relatively large in value, having a local charge source is critical to provide consistent and reliable operation. Typically, a power supply will be electrically far from the logic device, which results in a relatively large inductance and resistance between the power source and the device's supply pin.
Additionally, these sharp spikes can cause power disturbances for other devices on the same power network. We want to prevent this, so bypass capacitors are added.
Capacitor placement
Bypass capacitors should always be placed as close as possible to the device, electrically speaking. This means that you want to have wide, short traces and have the capacitor physically close to the device. It can be placed on the opposite side of the board to reduce distance if desired.
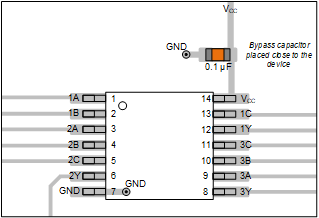
In general, it's better to place the capacitor close to the supply pin and connect the other side to a ground plane through a via, then provide a via to the ground pin of the device as well. There are other methods that work, but this is the most common and easiest to implement.
Example of bypass capacitor placement.
Selecting the right value of capacitor
It's important to understand that capacitors are real components that include non-ideal behavior. This is a commonly used model for real-world capacitors:
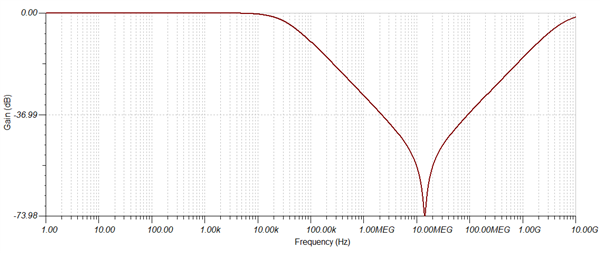
Of particular interest is the package inductance. If you recall the basics of inductors, they appear as open circuits at higher frequencies. This means that the capacitor will have an upper limit on the frequency range over which it can respond. Here's a plot of a capacitor's frequency response using typical values for a 0.1uF capacitor in a standard SMD package (1206).
* Note: This is not a plot for a particular capacitor, but a simulated response to show in general how capacitors respond.
The above plot is of gain vs frequency on a log-log scale (commonly called a Bode plot).The usable bandwidth for this capacitor ranges from approximately 100 kHz up to approximately 1 GHz (the "V" in the plot). At the lowest point, the capacitor has the lowest impedance, which is also the frequency at which it provides the most current (ie the fastest and best response). In this case, the capacitor provides the best performance just above 10 MHz.
* Note: The frequency plotted here is purely sinusoidal and relates directly to the edge rate of the logic signal - it is not related to the data rate or clock frequency of the signal.
-
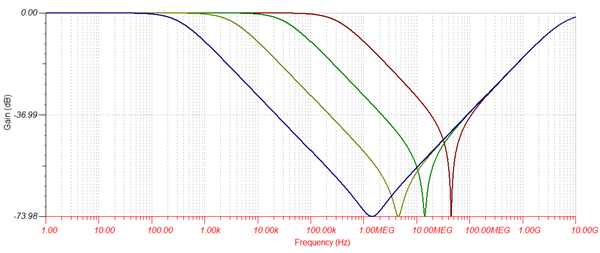
By varying the capacitance and holding other aspects constant, we can see how the capacitor value affects the response frequency:
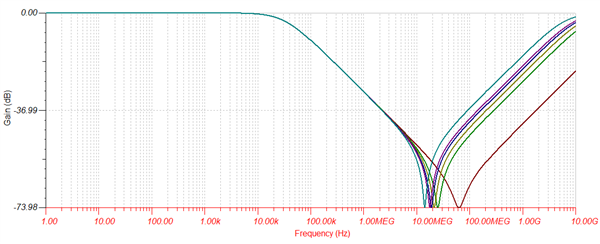
As the capacitor value is increased, the cutoff frequency on the low side decreases, while the cutoff on the high side remains constant. This is because the package inductance is being held constant while only the capacitance is changed.
-
If we vary the inductance instead by changing the package, we can see the opposite effect:
Reducing inductance by using a smaller package (or a package optimized for this application) will increase the corner frequency on the high-end of the plot, while the lower frequency will remain constant because the capacitance value is being held constant.
So, how do I select the best capacitor for my application?
* I'm not going to go into a lot of details on capacitor performance for particular packages and types -- considering that I work for TI and we don't make capacitors, I think this is a discussion better suited for a capacitor manufacturer. If you're interested in this topic in detail, there are multiple app notes and articles available on the web that go into great detail regarding this and are quite interesting and informative to read. I won't be linking any of them because I don't want to appear to recommend a particular manufacturer -- sorry about that. Google is a great resource to find these -- you can start with searching for "choosing a bypass capacitor."
There are two primary criteria for selecting the best bypass capacitor value in a particular application:
1. Expected signal frequency components
2. Expected loading - including number of channels simultaneously switching
(1) For the first criteria, we have to look at the spectrum of a signal. I'm not going to go into a lot of details on this, but let's just say that an ideal logic signal (square wave) has infinite frequency components, but a real-world signal will have limited frequency components (search "ideal square wave bandwidth" for details). These are primarily controlled by the edge rate of the signal -- generally speaking, logic devices produce signals with primary frequency components up to around 300 MHz. Please don't confuse this with the operating frequency -- you can have a 1 kHz signal that has 300 MHz frequency components because the edges are very fast.
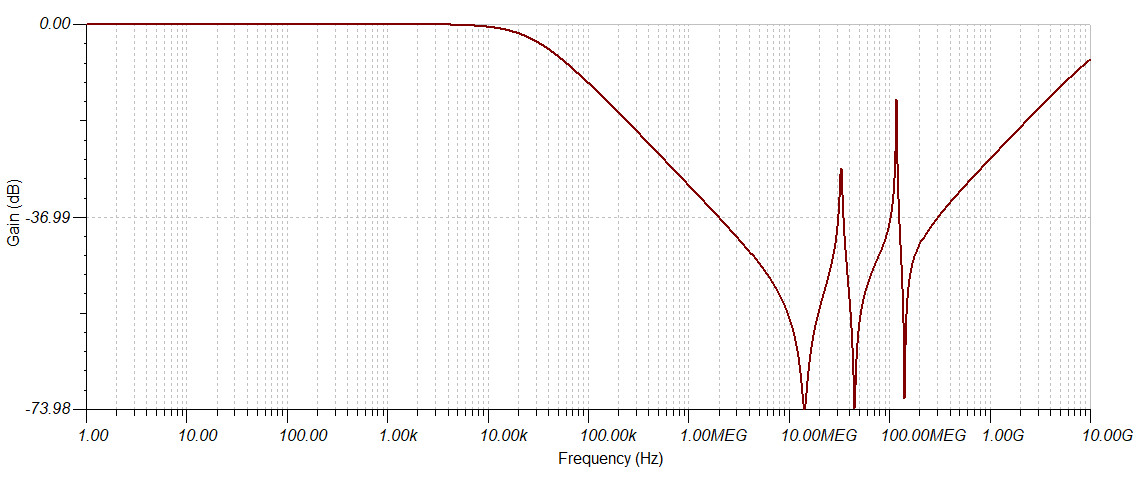
To ensure that you are able to source current as fast as necessary, the capacitor should have a bandwidth that includes as low of an impedance as possible at the desired maximum frequency. Generally speaking, a 0.1uF capacitor will cover a broad range of frequencies supporting from ~15 kHz to >1 GHz, however you can see from the above plots that it isn't optimized for a 300 MHz bandwidth signal. You could add additional parallel capacitors of smaller value to cover the higher frequency range. Here's an example using three capacitors in parallel of values 0.1uF, 0.01uF, and 1000pF:
(2) For the second criteria, we're looking specifically at how much charge is being drawn off of the capacitor with each switch of the output.
You can think of this in the context of charge sharing -- if you have a 0.1uF capacitive load on your logic gate, and you have a 0.1uF charge source for your power supply (with no other supply), then you would expect to get exactly half of the charge from your supply at the output, and thus your voltage at the output would be cut in half and half of the charge on your supply capacitor would be used up in the process.
Of course, the typical output load of a logic gate should be more like 10pF, so the charge sharing would be much different in a typical system. With a 10pF capacitor and 0.1uF bypass cap, the charge shared would result in 99.99% of Vcc at the output.
You wouldn't want to try to bypass the supply of a logic gate with only a 10pF capacitor, since that wouldn't be able to supply sufficient charge to the output. A a good rule of thumb is to keep your supply capacitor at least one order of magnitude larger than your output load. Again, a 0.1uF capacitor easily meets this criteria, so it's a good general purpose choice for a bypass capacitor.