Dear All,
Using an LM4F MCU at 80MHz (ADC 16MHz), it should be possible to sample repetitive signals at 16MS/s, and possibly higher, using ‘sequential equivalent-time’ sampling. This involves varying the time between the signal trigger and the ADC trigger so that a periodic signal which is too fast for the ADC (maximum 2MS/s ‘real-time’) can be captured over several cycles. The LM4F timers and wait-for-trigger (‘daisy-chain’) mode would look to be ideal tools here.
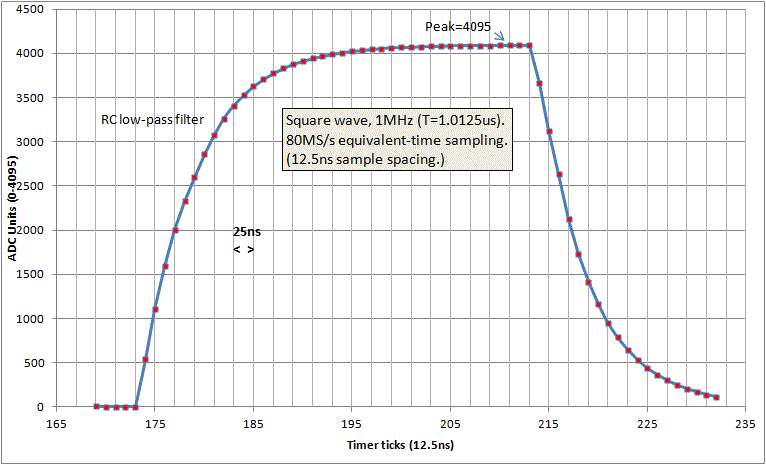
Initial results suggested that the timing resolution was not sufficient for 80MS/s (12.5ns), but after extracting more timing information, and re-arranging samples, I am able to demonstrate much higher resolution (<1ns).
Before going further though, I would like to understand more about the MCU/ADC behaviour beyond my ‘black box’ experiments. Any help/observations would be very welcome...
Here is the experimental setup:-
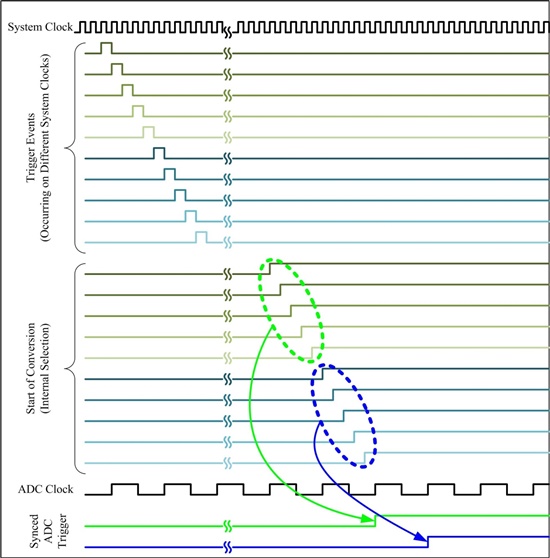
There are four timers in use for signals and sampling (I am using wide timers in 32-bit split-mode):-
Timers A1 and B1 use the wait-for-trigger (daisy-chain) mode to wait on timer B0 to timeout. A1, B1 are configured, pre-loaded, set into wait mode, enabled, and then fire on the next timeout of timer B0. This works very neatly except for a small limitation in daisy-chain mode – a timer must be reset (with ‘peripheral reset’) after each wait-for-trigger, which is a little untidy and will increase the sampling window time.
Using a ‘shadow’ signal (timer B0) with the same period as the PWM test signal means that triggering is guaranteed to occur, for the same offset, on exactly the same 12.5ns tick. If triggering depended instead on a signal on an input pin, then noise introduced onto the signal may introduce jitter. A second advantage is that the PWM test signal A0 can be moved in precise 12.5ns steps relative to the trigger B0. This is very useful feature for validating the accuracy of results, i.e. the trigger and ADC do not change, and the measured waveform should move by 12.5ns steps (which is demonstrated easily).
An ADC interrupt service routine first records the time B1, then reads the sample. The ‘conversion time’ from the initial trigger (B0 timeout) is then the B1 time plus the timing offset. Only one sample is collected per trigger event B0 for the experiments here (thus A1 in one-shot mode is sufficient).
With the MCU at 80MHz (ADC at 16MHz), and trying for 80MS/s, the sample values at a sharp pulse edge (e.g. 10-15ns) seemed to vary rather wildly (which might be expected), but I noticed that the same five values seemed to repeat themselves, and these matched up with the conversion time returned in timer B1.
What appears to happen is that for a fixed offset (12.5ns steps) in timer A1, the conversion time varies over five (12.5ns) steps (obviously 80/16). Recording ADC sample values against conversion time, instead of against time offset in timer A1, shows a highly correlated set of samples (see table below). A narrow, sharply rising/falling pulse is the most demanding test here, as just one tick (12.5ns) of timing jitter would destroy the coherence of the waveform at the transitions. To obtain a uniform distribution of times for one offset (in A1), it helps if a small random delay is added between each sampling event (e.g. using the low ADC bits to add a random delay of a few cycles).
Clearly the switch on the ADC sample-and-hold input circuit must open on a discrete 12.5ns step, and the conversion time returned (via B1) maintains this precision. Clearly also the interrupt latency (for the ADC ISR), plus any other latencies, are exactly the same every time (though it is possible that some incidental feature or interaction may be maintaining this precise latency, which would be a great shame!).
However, when the test signal period is a multiple of five timer ticks, only one time is returned, limiting the resolution to 16MS/s. The obvious explanation is that for a fixed offset, successive samples over several test signal cycles do not range over the five steps available inside a 62.5ns (16 MHz) interval, as they do when the period is not divisible by five. (For an external signal, this is less likely to be an issue in general.)
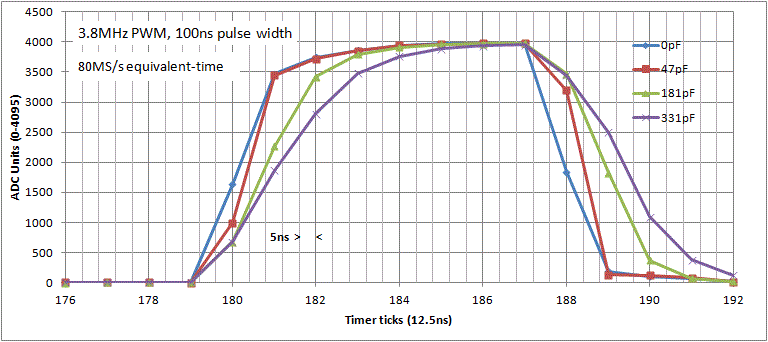
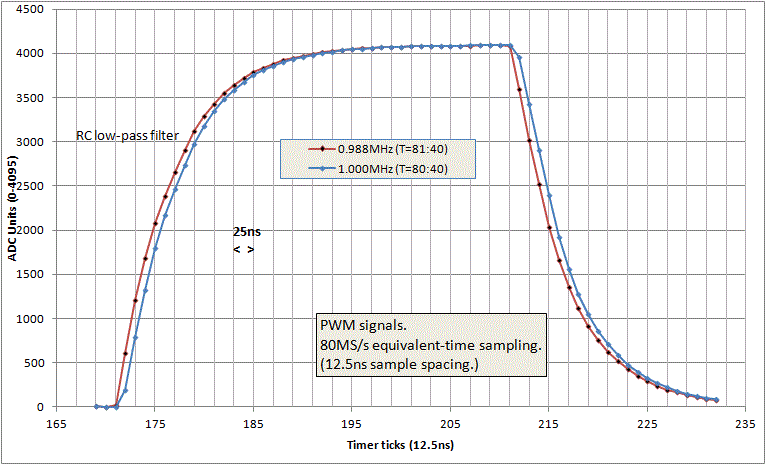
Here are results for 80MS/s equivalent-time sampling, with MCU=80MHz, test signal 3.8MHz PWM, pulse width 100ns (8 ticks at 80MHz), and drive 8mA into a (10R+1.5K) potential divider (to reduce the peak reading below 4095).
Key:
Here is the same PWM pulse (case C=0pF) along with pulses for a range of capacitance values between ADC input and GND :-
Now a good question is how meaningful are the ADC readings which catch the fastest pulse transitions, i.e. within the range 0-47pF? Rise/fall times of order 10ns would suggest rates of change here of 300V/us. As this is trying to track a change of about 400 ADC units in 1ns, the variation in the samples indicated by the rms value seemed too good to be believable. So, at first glance, I tended to dismiss the readings at the pulse edges, especially since the value returned can be different after a MCU reset (but begging the obvious question, why else should the samples be so consistent?).
An experiment using low capacitance values (0-47pF) to slow the signal rise and fall times very slightly (e.g. 1ns steps or less) should give distinct and repeatable readings just at the pulse transitions, if there is meaningful resolution available. Here are results using ceramic capacitors between the ADC input and GND for the rising and falling pulse edges (at t=180,188):-
These ADC sample mean values were surprisingly repeatable (e.g. +-2 ADC units) after re-inserting the same capacitor(s) (sometimes a day later!), and the plots show predictable movements. For each C value, the pulse was essentially the same shape (with peak =3980+-2) except at these two times. The rms error from the sample mean at the pulse transitions trends downwards with capacitance (typically 10-20rms for 0pF, 4-7rms for 47pF), the obvious explanation being that the signal rate of change is decreasing.
So this experiment suggests that within a range of about 5ns (see PWM pulse graph for t=180, 188), perhaps ten (and rather more) increments could be resolved, quite easily, by the timer/ADC sub-system, thus indicating a useful 0.5ns resolution. This was very surprising to me, but then I suppose the advantage with this configuration is that the test signal, trigger and the measurement sub-system are highly synchronized (and we have clocks available with a resolution of eight decimal digits!).
The ADC value recorded at a sharp transition seems to be consistent and repeatable after resetting timers, stopping and restarting the test signal and trigger timer (A0, B0) etc. But after a MCU reset, the transition samples can vary greatly (though resetting the MCU a few times will return eventually to the original values) – this suggests that the timer and/or ADC blocks may synchronize at slightly different points with the (master) PLL after a MCU reset, leading to a slight shift in time which is very obvious at any sharp transitions? (though I would need to look at this further.)
So whilst there is high resolution (<1ns) at sharp transitions, the absolute values there may be less meaningful (though calibration should be possible via a simple circuit to find the position). Anyway, the purpose of this small experiment was simply to estimate the timing resolution, which appears to be very good indeed.
So, the main conclusions are:
Quite high sample timing resolution (<1ns) would seem to be available using the timer and ADC blocks in the configuration outlined.
In general, a single ADC sample (at MCU=80MHz) can range over five distinct values with timing resolution about 50ns. (This is sufficient in many applications, but much higher resolution is possible.)
And some questions/observations:
Does the high sample timing resolution at 80MS/s rely on some incidental feature in the MCU/ADC? (A small modification might lose the data I am relying upon.)
Is there any way around the limit of 16MS/s when the signal period is a multiple of five timer ticks?
Is the behaviour of timer and ADC combination the same in the newer TIVA C MCU’s? (I can verify this later).
The daisy-chain mode timer must be ‘peripheral reset’ before each sample. This will limit the sampling window time.
Any help/comments would be much appreciated ...
Jim
----
Additional notes:
- The ADC is clocked using the PLL/25 option (default).
- The ADC module ‘sampling rate’ is 1MS/s. This setting is not critical, though lower rates will increase the total sampling window time.
- ‘ADC sample phase control’ will divide a 1MS/s interval into 16, so there is less resolution here than using the timer block.
- Some results were verified with a second EK-LM4F120XL board.
- The time per sample is 20us. This could be reduced with some optimization, and the daisy-chain timer limitation is an issue.
- Occasionally there is an empty time slot at 80MS/s, i.e. with no samples at all. This seems to depend on some internal MCU state.
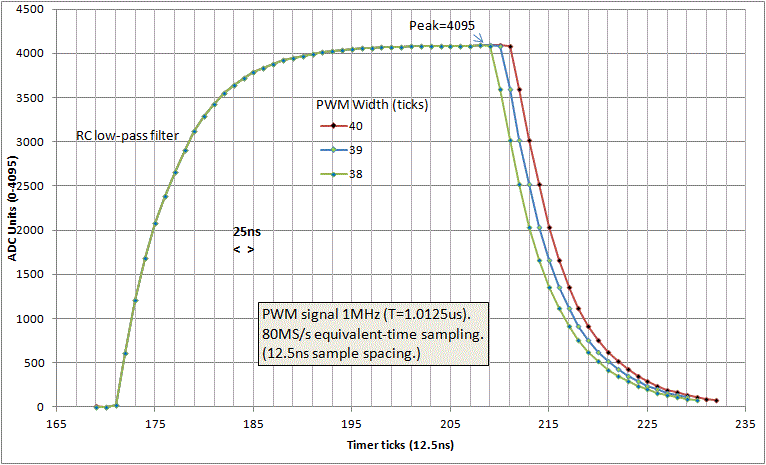
- Shifting the PWM signal in 12.5ns steps (by offsetting timer A0 relative to B0) has been demonstrated.