cFFT using CMSIS in the Tiva/Stellaris

Haroldo Amaral

Hi,

I'm starting to test/study the CMSIS lib in the Stellaris/Tiva. Using the paper "Using the CMSIS DSP Library in Code Composer Studio™ for TM4C MCUs", I got build the library and it works fine. The examples return the expected state.

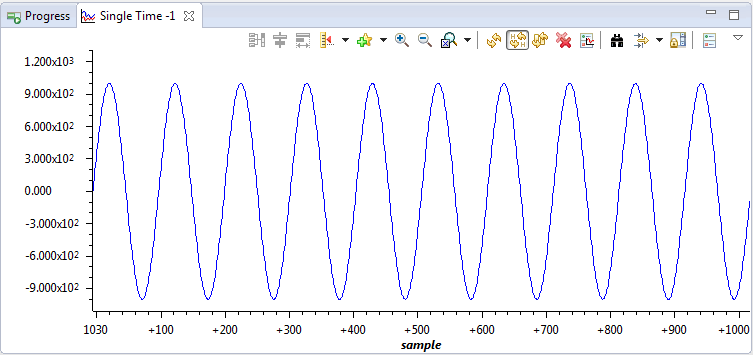
Now I trying to use the cFFT in a signal. To the test I created a pure sine wave in an array of 1024 samples (amplitude of 1000 and 10 cycles), as in the image.

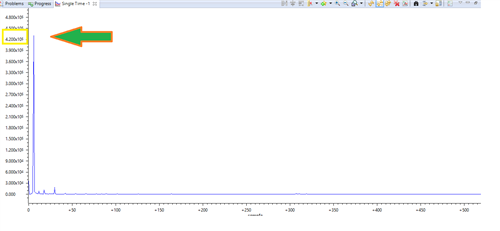
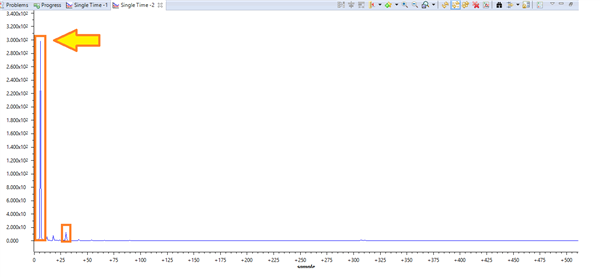
After the processing the indexer return the correct harmonic (10th), but I don't understand the result of the magnitude. The magnitude of the 10th hamonic is 727.98. How it relates to the amplitude of the harmonic?

This is the principal part of code:

#define		N_points	1024

...

uint32_t ifftFlag = 1;
uint32_t doBitReverse = 1;

/* Process the data through the CFFT/CIFFT module */
arm_cfft_f32(&arm_cfft_sR_f32_len512, wave_float, ifftFlag, doBitReverse);

/* Process the data through the Complex Magnitude Module for calculating the magnitude at each bin */
arm_cmplx_mag_f32(wave_float, wave_out, N_points/2);

/* Calculates maxValue and returns corresponding BIN value */
arm_max_f32(wave_out, N_points/2, &maxValue, &testIndex);

Thanks.

over 9 years ago

0 Amit Ashara over 9 years ago

TI__Guru**** 244400 points

Hello Haroldo

The arm_max_f32 returns the maximum of all the harmonics as given in the CMSIS documentation. Also do note that there is a new change to the application note that would be come online in the next couple of days,

Regards
Amit

0 Haroldo Amaral over 9 years ago in reply to Amit Ashara

Expert 1105 points

Hello Amit, thanks for the answer.

Yes, the function "arm_max_f32( )" returns the maximum value and the position in the array, as described in the documentation: "Computes the maximum value of an array of data. The function returns both the maximum value and its position within the array".

The indexer is ok, but I don't understand the value of the magnitude. I expected the value would be around 1000 (original amplitude).

I did a test doing the inverse fft, and the signal in the frequency domain was transformed in the time domain, with the original wave.

Can you tease what's new in the new version of document?

0 f. m. over 9 years ago in reply to Haroldo Amaral

Guru 11940 points

Actually, I don't know what the arm_cfft function returns in terms of power per "frequency bin". Since the CMSIS DSP lib comes from ARM and not TI, you might look at the ARM Infocenter websites for documentation.

At least I can remember that for FFTW (a PC based FFT library), each result had to be scaled by N (the number of input points) to get the power for each bin (after calculating magnitude/phase from real/imaginary, of course).

One way to test it would be transforming a reference signal (sinus, single frequency, range -1.0 .. +1.0). The result should tell you a required scaling factor, since one would expect about 1.0 (equaling 100%) for you reference frequency, ignoring windowing effects.

0 Haroldo Amaral over 9 years ago in reply to f. m.

Expert 1105 points

I tried to scale the sine wave between 1 and -1, but the result was the same. Instead of 727 the magnitude of the harmonic was 0.727.

It's strange because for different numbers of cycles the result of respective "bin" change.

Maintaining the same buffer size (1024) I changed to just one cycle and the result was around 708, very close to the RMS value. See this little list:

1024 samples
01 cycle -> 708.8323
02 cycles -> 710.9644
04 cycles -> 715.2491
08 cycles -> 723.74
16 cycles -> 740.4352

I tried to change the buffer size to 64 samples to test. In this case the result of one cycle was around 740.

I'm reading about how to obtain the amplitude, but in this moment I'm lost!

0 f. m. over 9 years ago in reply to Haroldo Amaral

Guru 11940 points

As said, I haven't looked at this (CMSIS DSP lib) in detail, perhaps ARM provides some more descriptive documentation.

But from the physical perspective, with a reference signal of a single frequency, the resulting power spectre should have about 100% of the spectral energy at the "bin" of your reference frequency, less some "spill-over" due to windowing and digitizing effects. The sum of all bins (of the power spectre) represents the total energy of the signal, so scaling the individual frequency bins to the power of a single-frequency/fullscale signal would make sense.

1024 samples
01 cycle -> 708.8323
02 cycles -> 710.9644
04 cycles -> 715.2491
08 cycles -> 723.74
16 cycles -> 740.4352

If "cycles" mean "cycles of the sine sgnal", this makes sense. Looks like you need to divide the individual bin values by the number of points, i.e. 1024.0.

The scaling of the result shifts with the scaling of the input signal - as one would expect. However, I would be wary of rounding errors - floating point has only 24 bits of accuracy, so you might be less precise than you think. Perhaps an evaluation of several variants (float / int / QMath) would make sense for you.

0 Amit Ashara over 9 years ago in reply to Haroldo Amaral

TI__Guru**** 244400 points

Hello Haroldo

An FFT works by taking a time domain signal to frequency domain. Due to the action of sampling the sine wave continuity is no longer valid, hence it creates harmonics in multiple of the fundamental frequency. What you are getting is the max value of the fundamental frequency. To double check the theory, increase the number of samples in the same time frame and then check what the max value is. It should be higher than what you have just received as the output.

The new version and support files is now online

www.ti.com/.../spma041g.pdf

Regards
Amit

0 Haroldo Amaral over 9 years ago in reply to f. m.

Expert 1105 points

f. m., yes, us the cycles of the sine signal.
Can you show an example of this processes.

0 Haroldo Amaral over 9 years ago in reply to Amit Ashara

Expert 1105 points

Hi Amit. I understand that the process of convert the signal introduce some distortion to the original signal. In this case I'm using a integer array to create the float array and simulate the behaviour of the quantization.

The idea is to find the fundamental value. If the original signal is "pure", the result of the respective bin would be the same? Why is bigger, and why increases with the increment in the number of cycles of the wave?

Yesterday I downloaded the new version. It's a little simple to configure the project. I have tested with version r4p2 and r4p3 and works well, I will test with the new r4p4.

Thanks

0 Amit Ashara over 9 years ago in reply to Haroldo Amaral

TI__Guru**** 244400 points

Hello Haroldo,

Yes, you are right. But sampling removes the "pure" part of the original signal. The signal reconstruction is now by interpolation. Having larger number of samples reduces the interpolation but cannot make it continuous unless N -> Infinity.

Regards
Amit

0 Martin Valencia over 9 years ago in reply to Haroldo Amaral

Guru 15175 points

Hi good day.
you are working with a discrete spectrum, so necessarily have to scale to your needs.
baby step:

1. capture the signal sample over time.
2. calculate the RMS value of the data sample.
3. calculate complex FFT
4. calculate magnitude of FFT.
5. seek the maximum value within the FFT (this value is the fundamental signal).
6. scalar, vector FFT with respect to its maximum value:
scaleFFT = FFT * 1 / max (FFT)
7. Multiply the vector scaling, the RMS value.
FFTrms=scaleFFT *RMS
8. FFTrms, has a scaling with respect to the RMS value vector.

Example:

1. capture the signal sample over time.

2. calculate the RMS value of the data sample.

3. calculate complex FFT
4. calculate magnitude of FFT.
5. seek the maximum value within the FFT (this value is the fundamental signal).

6. scalar, vector FFT with respect to its maximum value:
scaleFFT = FFT * 1 / max(FFT)

to this example, I gave a value of [ scaleFFT = FFT * 300/ max(FFT)], because my application requires it.

Free Sample Code:

/* Process the data through the CFFT/CIFFT module */
arm_cfft_radix4_f32(&S, Input_f32_3khz);

/* Process the data through the Complex Magnitude Module for
calculating the magnitude at each bin */
arm_cmplx_mag_f32(Input_f32_3khz, Output, fftSize);

/* Calculates maxValue and returns corresponding BIN value */
arm_max_f32(Output, fftSize / 2, &maxValue, &testIndex);

/* Scale the FFT */
arm_scale_f32(Output, 298 / maxValue, buffer, fftSize / 2);

0 Amit Ashara over 9 years ago in reply to Martin Valencia

TI__Guru**** 244400 points

Hello Martin,

Thanks for the very useful contribution. However it does not answer Haroldo's question which we are trying to explain and may be your insight into using CMSIS may lend a helping hand

FROM THE FIRST POST: "After the processing the indexer return the correct harmonic (10th), but I don't understand the result of the magnitude. The magnitude of the 10th hamonic is 727.98. How it relates to the amplitude of the harmonic?"

Regards
Amit

0 Haroldo Amaral over 9 years ago in reply to Martin Valencia

Expert 1105 points

Just more one question Martin Valencia.

In this part of code "arm_scale_f32(Output, 298 / maxValue, buffer, fftSize / 2);" - the value "298" in your project is related to the maximum projected value? Amplitude or RMS?

0 Martin Valencia over 9 years ago in reply to Haroldo Amaral

Guru 15175 points

It has no relation with RMS; This value is selecione for my project.

I use 300 pixels high to plot the frequency spectrum of a square wave.
to avoid me unnecessary calculations; I multiply 298 pixels high.

here image:

for your application:

arm_scale_f32(Output, Vrms/ maxValue, buffer, fftSize / 2);

if you want to know what the energy of 10th harmonic , simply divide

Energy_n = (Harmonic [10] / Harmonic [1]) * 100%

the result interprets it as:

the 10th harmonic has value% with respect to its fundamental

0 Haroldo Amaral over 9 years ago in reply to Martin Valencia

Expert 1105 points

Thanks for everyone that contributed in this post, was very helpful to me.

I will try the new version of the headers from TI and report the result.

0 Haroldo Amaral over 9 years ago in reply to Amit Ashara

Expert 1105 points

Amit you're right, Martin's reply does not solve the problem completly, but guided me the solution.

The function "arm_scale_f32(Output, 298 / maxValue, buffer, fftSize / 2);" scale the magnitudes, in this case the maximum value will be 298 (specific Martin's case).

In my problem I need measure the respective value of each harmonic and the unique reference value is the RMS value from the original wave.

If I do this "arm_scale_f32(Output, RMS / maxValue, buffer, fftSize / 2);", the fundamental will be scaled to the RMS value. To solve this it is necessary to calculate a correction factor to be applied. This factor takes into account the quadratic sum of the harmonics after the fundamental. The function will look like "arm_scale_f32(Output, (RMS / maxValue) * correction_factor, buffer, fftSize / 2);"

Now, I'm thinking it's possible to use the formulation without the correction factor, after the scale calculte the RMS with the magnitudes, then calculate the correction factor and scale again using this factor.

0 Martin Valencia over 9 years ago in reply to Haroldo Amaral

Guru 15175 points

Thank you very much for your feedback!
I hope you can share the final result of your application, Greetings!

Arm-based microcontrollers

Arm-based microcontrollers forum

cFFT using CMSIS in the Tiva/Stellaris