• State
  • Locked Locked
  • Replies 6 replies
  • Subscribers 84 subscribers
  • Views 368 views
  • Users 0 members are here
Support feedback
Options
Options
Related

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

Original question:

TMS320F28379D: Can I change ePWM up-down counting direction online?

TMS320F28379D: Implementing code on faster tasks

mike buba
Intellectual 470 points
Part Number: TMS320F28379D


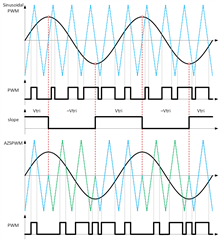
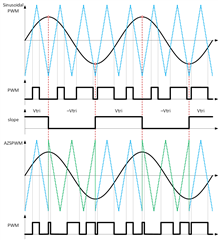
Hi, is it possible to implement a custom algorithm on a faster task, e.g., the task on which the ePWM block is executed?

I have successfully implemented the solution from here, but I noticed the "accuracy" depends on the sample time. I'll try to explain:

When the slope change is detected, the counter value (ePMW's TBCTR) is recorded and if the slope is rising there is no change to phase offset and TBPHS = TBCTR, and if the slope is falling TBPHS = TBPRD - TBCTR (180 Deg shift).

  CounterShift_R2018a_v000.zip

What I noticed is that the accuracy depends on my application sample time. In some cases the counter slope change (Ch4) corresponds to the slope change digital signal (Ch1), and in other cases, it is shifted by several periods. Both figures are recorded during the same run. It ca be seen that there is a delay between the slope change signal and the actual counter slope change and also the slope change does not happen at the 'same' time.

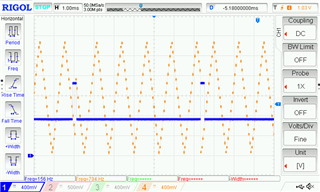
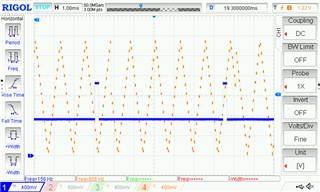
  • Ch1: slope change signal
  • Ch4: ramp signal (counter value)

In other cases, the sections are not shifted by 180 Deg. Ch3 and Ch4 signals should be in phase where there is no slope change signal, and 180 Deg shifted when there is a slope change. But the figure shows they are not in phase and even between two slope change events are not shifted by the same angle.

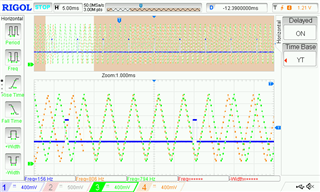
  • Ch1: slope change signal
  • Ch3: counter signal from another ePMW with the same settings
  • Ch4: ramp signal (counter value)

Is this possible to implement this algorithm on some faster ePWM task? Is there any other approach I could try?

This example is done for a switching frequency of 800 Hz. For 50 μs task's sample time, this gives 25 points per switching frequency period (counter). If I go to any higher frequencies, e.g., 8 kHz, the application would read only 2.5 points for each switching frequency period (counter), which is too little for the algorithm at the current sample time to work properly. If I increase my the sample task time, I get overflow

  • 0
    TI__Mastermind 27736 points

    Hi Mike,

    I will take a look into this, and get back to you by end of day. 

    Best, 

    Ryan Ma

  • 0
    TI__Mastermind 27736 points

    Hi Mike, 

    What do you mean by a "custom algorithm on a faster task". Do you mean you want a faster way to execute your ISR handler with your custom algorithm? 

    Ch1, is that supposed to toggle everytime CH4 changes its slope? I.e. When ch4 is going down, CH1 should toggle, then going up CH1 will toggle again. How come it only toggles every 4 or so periods? Is this done on purpose?

    I believe I am understanding the problem here,

    In that bottom picture, when CH1 toggles... CH4 and CH3 seem to be in sync because CH4 is slope is going up. However when CH4 slope changes to go down, CH3 and CH4 do not seem to be phase shifted by the expected 180 degrees.

    What is your TBPHS value when the slope changes to go down or up? Can you verify that the TBPHS register has your expected value when it should be 180 degrees phase shift value when slope is going down? 

  • 0 in reply to Ryan Ma
    Intellectual 470 points

    Hi Ryan,

    the algorithm changes the counter slope every time the sinusoidal reference slope changes. Ch1 is the sinusoidal slope change signal and initiates the counter slope change, i.e. writes a new value in TBPHS Phase Offset Register.

    The algorithm works like this: every time the sinusoidal slope changes, Time Base Counter Register value (TBCTR) is recorder. If the sinusoidal slope is positive, recorded TBCTR is copied to the offset register TBPHS , i.e. no change. If the sinusoidal slope is negative, the offset register is  set to TBPRD - recorded TBCTR.

    Figures below illustrate how the ramp slope change should behave.

    Ryan Ma said:

    In that bottom picture, when CH1 toggles... CH4 and CH3 seem to be in sync because CH4 is slope is going up. However when CH4 slope changes to go down, CH3 and CH4 do not seem to be phase shifted by the expected 180 degrees.

    What is your TBPHS value when the slope changes to go down or up? Can you verify that the TBPHS register has your expected value when it should be 180 degrees phase shift value when slope is going down? 

    TBCTR values I am sending to the TBPHS at the counter change trigger are not 100% as expected, but they are not wrong either. It seems there is a drift. They are not the same as the previous value, or value before that. From time to time I get a correct match, most of the time it is not 180 Deg shift. This can be seen also in this figure. It starts with the ~180 Deg offset, then goes to ~0 Deg offset, but after that it is not ~180 Deg offset.

     

    Ryan Ma said:
    What do you mean by a "custom algorithm on a faster task". Do you mean you want a faster way to execute your ISR handler with your custom algorithm? 

    Yes. If I increase the resolution (going from 20e-5 to 10e-5 sample time) at which I am recording TBCTR, I get less discrepancy between the numbers. But lower sample time leads to overrun. PWM ramp in this example is 800 Hz and the finial value should be 8 kHz. Executing the algorithm faster seems to improve the accuracy. Or are there some other ways of improving.

  • 0 in reply to mike buba
    TI__Mastermind 27736 points

    Hi Mike,

    Sorry I am unable to provide an answer today. I will follow up with you tomorrow on this.

    Best,

    Ryan Ma

  • 0 in reply to mike buba
    TI__Mastermind 27736 points

    Hi Mike, 

    I can loop in an interrupt expert to see how we can optimize your ISR handler.

    A few things I want to ask is, how are you compiling your code? Under Project > Properties > C2000 Compiler > Optimization you can customize the level of how your code gets compiled. By increasing for speed, could you see if this helps first?

  • 0 in reply to Ryan Ma
    Intellectual 470 points

    Hi Ryan,

    apologies for the late reply. I tried to the code optimization. I even tried to run 'only' ePWM block + my code for slope shift, but still getting the same issue. I also tried to understand why is this happening. 

    The best explanation I could come up with is:

    When the slope change event appears (Ch1), time t1 passes when the TBCTR value is read and saved to be written in TBPHS for slope change.  TBCTR still increases unilt t2 passes and only then slope change takes effect, i.e. TBPHS register is refreshed and ePWM starts counting from TBPHS. It takes several samples to execute. My rationale for the question (Implementing code on faster task)  was if I increase the sample time, t1 and t2 would reduce.

    The idea for the algorithm is suggested here; as soon as the change event appears, TBCTR should be recorded and ePWM should re-start from TBPHS. 

    Can you please advise if interrupt (or advice from interrupt expert) could help me move forward?