- Ask a related questionWhat is a related question?A related question is a question created from another question. When the related question is created, it will be automatically linked to the original question.
This thread has been locked.
If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.
Hi Chris,
It is stated that the FAST estimates the rotor flux and the rotor angle.
what do you mean by rotor flux ?
For example, in PMSM/synchronous motors, if you write the stator equations in the rotor frame, you get the stator flux in the rotor frame... I'm not familiar with the term "rotor flux"...
Q:
1. can you please explain the term "rotor flux" with respect to the motor equations (I assume stator voltage equation in the d-q frame attached to the rotor)
2. is it possible to calculate the "load angle" - that is, the angle between the stator flux vector and the d-axis of the rotor, from estimated variables ?
thanks a lot
Mojo,
Rotor flux is the flux linkage between the rotor and the stator, and we give this value in Volts per Hz or Webers (Volt seconds).
The "rotor angle" is actually the angle of the rotor flux.
This is rotor frame referenced, meaning the relative angle is aligned with the Id axis in the d-q frame that rotates with the rotor flux.
Based on this rotor flux angle, an angle is calculated for the vector of the stator flux that you want to create - typically 90 degrees leading based on rotational direction - and defined by an Iq and Id value in the rotating d-q frame.
Hi Mojo,
On a PMSM, the rotor flux is simply a measure of the flux density (i.e., magnet strength) of the magnets attached to the rotor while it is inserted in the stator frame. I see that you are familiar with the PMSM stator voltage equations for a system where the d-q frame is attached to the rotor. But at what angle is it attached to the rotor? In most cases, it is attached at the angle where the north pole of the rotor magnet is pointing to. This is called the rotor flux axis, and this is what we usually line up the d-axis with. With InstaSPIN-FOC (as with most FOC algorithms), we are not really concerned with the true rotor flux, since the part of the flux from the magnets that doesn't link to the stator is irrelevant since it doesn't produce any voltage or torque. When we say "rotor flux", we are really talking about the portion of the rotor flux that jumps the airgap and interacts with the stator. This is called the rotor flux linkage, which is usually denoted by the symbol lfd. In fact, the rotor flux linkage plays a large part in determining the d-axis stator flux, as seen from the equation below:
d-axis stator flux = rotor flux linkage + stator inductance * d-axis stator current.
More importantly, the motor torque can be calculated by simply multiplying the rotor flux linkage times the q-axis stator current times the number of rotor poles/2. This is how InstaSPIN-FOC calculates torque, and is one of the reasons why we need to accurately determine the amplitude of the rotor flux linkage.
With regard to your second question, please be mindful that the stator current mmf vector is NOT the same as the stator flux vector. Having said that, the answer to your question is "yes". Using the equation above, we can calculate the d-axis stator flux. The q-axis stator flux is defined below:
q-axis stator flux = stator inductance * q-axis stator current.
The MotorID portion of InstaSPIN-FOC measures the stator inductance and the rotor flux linkage. The FAST portion of InstaSPIN-FOC determines the real-time values of the d and q axis stator currents. From this you can calculate the d and q axis values of stator flux. Then you can use rectangular to polar conversion to find the angle of the stator flux w.r.t. the d-axis.
-Dave
...small correction to my last post.
Rotor flux (or flux in general) is a measure of the number of magnetic lines of force being created by the magnetic field in the rotor, and is measured in units of Webers. "Flux density" is obviously the density of these "lines of force", which is measured in units of flux per area. 1 Weber of flux lines cutting through1 square meter of area creates a flux density of 1 Tesla. Incidentally, Webers is numerically equal to the back-EMF constant of a PMSM machine in SI units.
Sorry for the confusion,
Dave
Hi Dave,
thanks for the through response.
however, you got me confused. From your first paragraph, I was sure that you're using the air-gap flux linkage reference frame...
then, from the equation -> d-axis stator flux = rotor flux linkage + stator inductance * d-axis stator current
I understand you are talking about the rotor flux linkage reference frame...a little bit confusing....
A phasor diagram here will solve the question, I think. I would appreicate if you can post such a diagram, specifying the angles, vectors etc. this is the most understandable explanation, as I see it...
furthermore, what I fail to understand is :
1. why trying to estimate the rotor flux linkage, since it is constant. you state that you need the ampltude for the torque, but if it's constant...
2. you stated that instaSPIN-FOC calculates the torque as : rotor_flux*Iq. this, however, is a very very short expression of the whole... in case of salient pole, or synchronous motor with dampers..
your comments are mostly appreciated,
thanks
Hi Mojo,
Sorry for the confusion. All we are doing is rotor flux referenced field oriented control. From my travels, I have come to believe that this is the most popular type of field oriented control. So there is really nothing magical we are doing in this respect. If this is not something you are familiar with, I can provide several good references on field oriented control where this is discussed in detail.
In an attempt to clear up some of the confusion, I drew a phasor diagram as you requested.
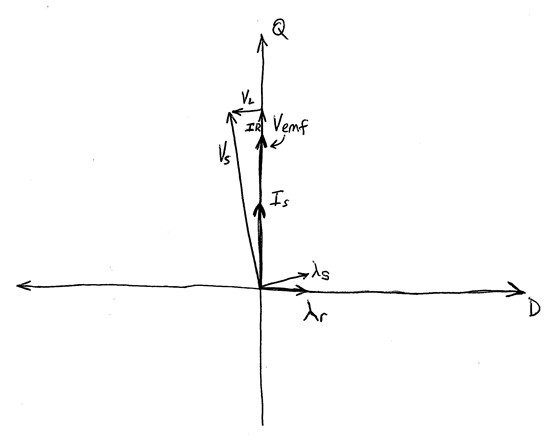 As you can see, the d-axis is aligned with the rotor flux, which implies that for precise field-oriented control, the back-emf vector will be on the q-axis, along with the stator current vector. The stator voltage vector is found as the vector addition of the back-EMF vector, the IR voltage drop vector from Rs, and the stator inductance voltage drop.
As you can see, the d-axis is aligned with the rotor flux, which implies that for precise field-oriented control, the back-emf vector will be on the q-axis, along with the stator current vector. The stator voltage vector is found as the vector addition of the back-EMF vector, the IR voltage drop vector from Rs, and the stator inductance voltage drop.
It turns out the the rotor flux linkage is anything but constant. On AC induction machines, it is a controlled parameter which is used to enable high-speed operation. Our FAST observer can track this perfectly for applications such as field weakening. But even with a permanent magnet machine, the variability of the flux linkage is a function of the type of magnet material that is used. This is related to the hysteresis curve of the magnet. We have seen substantial variations in the rotor flux linkage on cheap motors as you start loading them down. Again FAST tracks this perfectly, allowing it to still achieve an accurate torque estimate, or even to dynamically readjust your loop tuning parameters in extreme cases. But even rare-earth materials like Neodymium Iron Boron will still experience some degree of flux variation as a function of stator current level.
With regard to your second question, I provided the torque expression for a PMSM machine that is considered to be "magnetically round" (i.e., no saliency); and yes, that is the whole expression. For other types of motors, we alter the torque expression to include other terms (such as the reluctance torque in IPMSM machines).
-Dave
Hi,
I would like to implement a BEMF feedforward compensation. That is:
Uff_d = -w*Psi_q
Uff_q = w*Psi_d
where the stator flux linkage is of course:
Psi_q = Lq*Iq => [H]*[A]
Psi_d = Psi_rotor+Ld*Id => [Weber]+[H]*[A]
w=rotor electrical frequency [rad/sec]
My questions are:
1. Which variables / terms in the Motorware software do you suggest on using for calculation of the different terms of the stator flux linkage ? I'm a little bit lost with all the units (p.u,volt/Hz etc).
2. In order to combine into the controller, some sort of per-unit transformation is needed (after calculating Uff in SI unit, I need to convert to p.u). How do you suggest on doing that ? (I thought just to use Uff/MAX_VOLTAGE, as set in user.h)
thanks a lot
Hi,
You can use the following global variables:
_iq gLd_H;
_iq gLq_H;
_iq gId_A;
_iq gIq_A;
_iq gPsi_rotor_VpHz;
_iq gPsi_d_VpHz;
_iq gPsi_q_VpHz;
_iq gUff_d_pu;
_iq gUff_q_pu;
And then, run this code:
gLd_H = _IQ(EST_getLs_d_H(obj->estHandle));
gLq_H = _IQ(EST_getLs_q_H(obj->estHandle));
gPsi_rotor_VpHz = _IQ(EST_getFlux_VpHz(obj->estHandle));
gId_A = _IQmpy(CTRL_getId_in_pu(handle),_IQ(USER_IQ_FULL_SCALE_CURRENT_A));
gIq_A = _IQmpy(CTRL_getIq_in_pu(handle),_IQ(USER_IQ_FULL_SCALE_CURRENT_A));
gPsi_d_VpHz = gPsi_rotor_VpHz + _IQmpy(_IQmpy(gLd_H,gId_A),_IQ(2*MATH_PI));
gPsi_q_VpHz = _IQmpy(_IQmpy(gLq_H,gIq_A),_IQ(2*MATH_PI));
gUff_d_pu = _IQmpy(gPsi_q_VpHz,_IQmpy(EST_getFe_pu(obj->estHandle),_IQ(USER_IQ_FULL_SCALE_FREQ_Hz/USER_IQ_FULL_SCALE_VOLTAGE_V)));
gUff_q_pu = _IQmpy(gPsi_d_VpHz,_IQmpy(EST_getFe_pu(obj->estHandle),_IQ(USER_IQ_FULL_SCALE_FREQ_Hz/USER_IQ_FULL_SCALE_VOLTAGE_V)));
A couple of comments on this code:
I hope this helps!
-Jorge
Hi Jorge,
Thanks a lot for the code snippet !
One question please - why do you multiply by 2*PI:
_IQmpy(_IQmpy(gLd_H,gId_A),_IQ(2*MATH_PI))
thanks again, It very helpful
Hi,
I multiply to get the flux in V/Hz. So in V/Hz:
gPsi_rotor_VpHz = _IQ(EST_getFlux_VpHz(obj->estHandle));
gPsi_d_VpHz = gPsi_rotor_VpHz + _IQmpy(_IQmpy(gLd_H,gId_A),_IQ(2*MATH_PI));
gPsi_q_VpHz = _IQmpy(_IQmpy(gLq_H,gIq_A),_IQ(2*MATH_PI));
In Wb:
gPsi_rotor_Wb = _IQ(EST_getFlux_Wb(obj->estHandle));
gPsi_d_Wb = gPsi_rotor_Wb + _IQmpy(gLd_H,gId_A);
gPsi_q_Wb = _IQmpy(gLq_H,gIq_A);
-Jorge
Hi Jorge,
2 comments:
1. Since Uff_d = -w*Psi_q, there should be a minus sign (-) when calculating Uff_d - i.e
-(_IQmpy(gPsi_q_VpHz,_IQmpy(EST_
getFe_pu(obj->estHandle),_IQ(USER_IQ_FULL_SCALE_FREQ_Hz/USER_IQ_FULL_SCALE_VOLTAGE_V))));
2. If using floating point builds, then the flux value should be obtained using the union interface:
union
{
int32_t long_value;
float_t float_value;
} interface;
interface.long_value = EST_getFlux_VpHz(obj->estHandle);
gPsi_rotor_VpHz = _IQ(interface.float_value);
correct me if I' wrong...
Yes, I agree on the negative, although you can keep the operation positive, and subtract it from the output of the current controller, your choice.
Yes, you are also correct on the floating point build using a union.
-Jorge
Hi Jorge,
So as you said, the function EST_getFlux_VpHz takes forever to run (40us to be more accurate...)
Since I would like to get the flux in the ISR, I tried using EST_getFlux_pu as following (taken from TI code in est.h):
#define VarShift(var,nshift) (((nshift) < 0) ? ((var)>>(-(nshift))) : ((var)<<(nshift)))
_iq Flux_Wb;
_iq Flux_pu = EST_getFlux_pu(obj->estHandle);
_iq FullScaleFlux = _IQ(USER_IQ_FULL_SCALE_VOLTAGE_V/USER_EST_FREQ_Hz);
uint_least8_t Flux_qFmt = EST_getFlux_qFmt(obj->estHandle);
_iq scale_factor = VarShift(FullScaleFlux, Flux_qFmt - 30);
Flux_Wb = _IQmpy(Flux_pu, scale_factor);
gPsi_rotor_VpHz = _IQmpy(Flux_Wb, _IQ(6.28)); // 6.28 is 2*pi
This code indeed runs faster (less than 1us).
However, I don't get same value when calculated as the above code (I got 0.035 V/Hz) and when using EST_getFlux_VpHz (I get 0.019 V/Hz, which is correct, and this is also the value when running the Motor ID)
Is the above method correct ?
why is there a difference ?
Thanks a lot
Mojo,
We have just confirmed this is a bug with getFlux_pu() and EST_getFlux_qFmt()
This will return the wrong value through MotorWare _11 at a minimum (likely _12 as well).
We will see if this is something we can patch outside the ROM for future release. For now the only proper way to get Flux is to request it in your non time critical code with the EST_getFlux_VpHz.
Hey Dave,
firstly thank you so much on that great explanation on what rotor flux and rotor flux linkage is, that clarified a lot. I would like to know if you could also explain what is meant by weakening the rotor flux linkages?
Reagrds,
Greg.
Hi Greg,
Unfortunately I can't see my explanation you are referring to, so I don't know what I may have already said related to this topic. But no matter...I'm glad you found it to be helpful.
As the rotor spins inside the set of stator coils, it induces a back-EMF voltage resulting from d-flux/dt. This means that as the rotor spins faster relative to the stationary stator coils, this back-EMF voltage increases. You soon reach a point near the full-speed rating of the motor where the back-EMF voltage is so high, it inhibits the ability of the applied voltage to produce current, and the motor cannot go any faster.
At this point, you have two choices: 1) Increase the applied voltage, or 2) Decrease the back-EMF voltage. In many cases, increasing the applied voltage is just not economically practical. So most designers choose to reduce the back-EMF voltage. This is done by passing a current through the stator coils at just the right spatial angle so as to create a counter-flux in the stator coil which opposes the original flux linked from the rotor magnet. Since the stator coil's net flux linkage is reduced, the d-flux/dt is also reduced for a given speed. It turns out that in a field-oriented system, the optimum spatial angle to apply this stator current is along the axis which the rotor flux is currently pointing. In other words, along the d-axis. So, in order to oppose the rotor flux, we must supply a negative current on the d-axis.
One very common misconception about field weakening (at least with permanent magnet machines) is that fleld weakening reduces the rotor flux. this is not true. The rotor flux is established by the field strength of the rotor magnets, and is "permanent". What we are doing is reducing the flux that links into the stator coils. Therefore, as a result of field weakening, you motor can achieve speeds that are higher than the rated speed of the motor, but at a cost of reduced efficiency due to the extra stator current required to do this.
Best Regards,
Dave