Hi,
I am trying to implement FFT algorithm for Real Input disucssed on wiki page given below.
http://processors.wiki.ti.com/index.php/Efficient_FFT_Computation_of_Real_Input
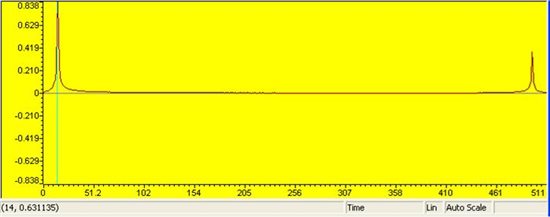
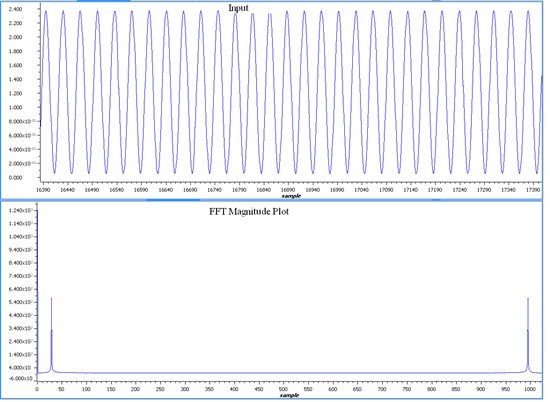
But I am not getting the right result, it has 3 peaks which can be observed in the figure given below.

Moreover, FFT magnitude is not showing the right amplitude as of input signal which is 1.25V. I will really appreciate if some one help me out here.
Regards.
Tariq