• State Resolved
  • Locked Locked
  • Replies 10 replies
  • Subscribers 100 subscribers
  • Views 1664 views
  • Users 0 members are here
Support feedback
Options
Options
Related

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

[C674x] clocks for math operations (sqrt and pow)

Hayden Kim
Genius 15580 points
Other Parts Discussed in Thread: TMS320C6746, MATHLIB

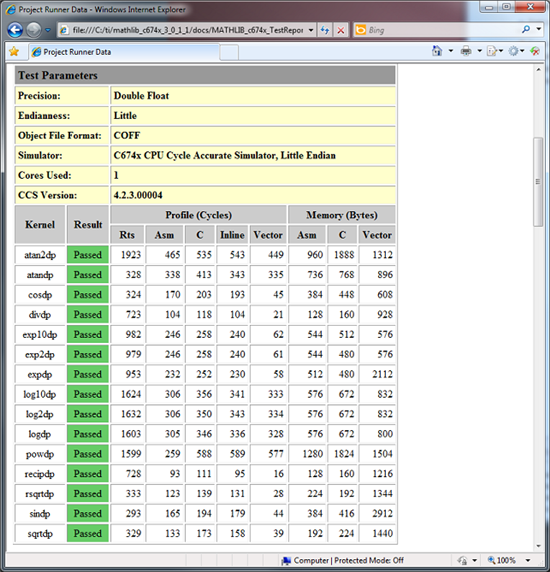
With C674x DSP (TMS320C6746), can I know the required clock cycles for below math operations?

  * sqrt ( double A ) =

  * pow (double A, double B) =

And, what is the fastest way (for the performance) to do above math operations?

Thanks and regards.

Hayden Kim

  • 0
    Intellectual 600 points

    if an approximation is sufficient for your needs you can use the C674x intrinsics. each of them is two cycle command.

    double Asqrt = _rcpdp(_rsqpdp( A));

    see SPRUFE8B for details.

  • 0 in reply to 1768011
    TI__Genius 15580 points

    According to the test report of MATHLIB (mathlib_c674x_3_0_1_1), the test results are like below table.




    * powdp costs 259 cycles with "Asm".

    * rsqrtdp costs 28 cycles with "Vector".


    Os, can you explain about this table of test results?


    Thanks and regards,

    Hayden

  • 0 in reply to Hayden Kim
    TI__Guru** 116170 points

    Hi Hayden,

    ASM function benchmarks correspond to average cycle count taken by the function when called for a single value. Vector benchmarks correspond to average cycle count per sample in the vector when the function is iteratively applied to all the samples of the vector. This benchmark generally shows better results as the compiler parallelizes the code over the available DSP resources by software pipelining the code.

    Regards,

    Rahul

  • 0 in reply to Rahul Prabhu
    TI__Genius 15580 points
    Thanks for answers.
    What I actually want to know is to estimate cycles of below calculation.

       (double) result = sqrt( (1.2 * 1.5) + pow( (1.3 / 3), 2.5 ) );

    Can you give the estimated cycles?

    Regards,
    Hayden
  • 0 in reply to Hayden Kim
    TI__Guru* 84110 points

    Hayden,

    What do you want or need the answer to be?

    For this exact example, the operations must be done serially. You can choose any column from the table you posted above, but not the vector column. Add the numbers from the column you selected and that is your answer.

    If you need the answer to be different from that, then you will need to explain more about the application in which you will be using this math.

    Regards,
    RandyP

  • 0 in reply to RandyP
    TI__Genius 15580 points

    Hi RandyP,

    I asked because "rsqrdp" instruction consumes only 2 cycles, but "rsqrtdp" at the table shows 123(Asm), 131(Inline) cycles.

    Why does it show big difference?

    Regards,

    Hayden

  • 0 in reply to Hayden Kim
    TI__Guru* 84110 points

    Hayden,

    This is very confusing. This is the first time you have mentioned rsqrdp. It is a different function from rsqrtdp, so it takes a different amount of time. Multiply and divide operations take different amounts of time between each other. Complex Dot Product and Complex FFT take a different amount of time, even though they both have "complex" in the name.

    Have we answered your questions?

    Regards,
    RandyP

  • 0 in reply to RandyP
    TI__Genius 15580 points

    My goal of this question is to know the fastest method of "sqrt()" and "pow()" calculation and the estimated cycles, as the question of beginning.

    If rsqrdp takes 2 cycles and rsqrtdp takes 130 cycles with same result value, who will use rsqrtdp?

    It will be good if there is some explanation for the understanding.


    Regards,

    Hayden

  • 0 in reply to Hayden Kim
    TI__Guru* 84110 points

    Hayden,

    _rsqrdp is a compiler intrinsic that directs the compiler to use a specific instruction. The RSQRDP instruction is explained in the C674x CPU & Instruction Set Reference Guide. It returns an approximate value for the reciprocal square root.

    The rsqrtdp is an implemented function that cacluates the full 64-bit-accurate value, not approximate, for the reciprocal square root.

    There may be a way to use iteration to get more accuracy with a few calls to the _rsqrdp intrinsic, but this may not be how the rsqrdp() function works.

    They return different accuracies, so my analogies above were incorrect.

    _rsqrdp is fast, while rsqrdp() is accurate.

    _rsqrdp is not easily portable, while rsqrdp() can be easily ported to another architecture.

    Regards,
    RandyP

  • 0 in reply to RandyP
    TI__Genius 15580 points

    Thanks for the explanation.

    Regards,

    Hayden