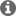Other Parts Discussed in Thread: AWR1642
Hi,
1- This refers to the previous question fro RCS Calculation / Estimation. I have gone through and understood the previous question. I have some additional queries and request guidance of TI team or some other user on the following points. I am deliberately stating the steps that I have carried out. I request you to please go through them, if you find them right, please comment ok and/or extend additional advice if you feel so. If you see them wrong then please advise the right way.
I am using AWR1642BOOST + DCA1000 EVM to capture raw ADC data. I am storing it on a PC and processing it with readDCA1000 MATLAB script provided by TI. This script is producing a matrix of complex values. I am trying to further process this data in MATLAB to have estimate of target Radar Cross Section (RCS).
2- Please refer page 50 on TI mmwave training pdf file. The screen shot is as follows:
 3- As indicated int he previous post, I intend to keep all other parameters constant and thus I expect to obtain an estimate of RCS from the SNR values.
3- As indicated int he previous post, I intend to keep all other parameters constant and thus I expect to obtain an estimate of RCS from the SNR values.
4- In many standard Radar Texts, an additional term "Losses" is included in the denominator of the above equation. However, no such term in included in the above equation. Does TI consider extending advice that should I consider adding the Losses in the above equation to have more realistic and accurate results ? If yes, then what system losses TI could consider advising ? Or, does the equation give a fairly optimal result even without inclusion of losses term ?
5- I understand that if I use decibel arithmetic for solving the above SNR equation (as commonly and conveniently done in radar calculations) then I must add the antenna gain dB values for transmitter and receiver in SNR equation (addition in dB is analogous to multiplication in linear units). AWR1642BOOST EVM User Guide (swru508b) states peak gain of 10 dB both for the transmitting and receiving antennas.
Please advise that should I add two antenna gains if I use two transmitters AND should I, for example, add 2 receiver gains if I use two receivers ?
6- The above equation includes a term lambda (wavelength). We know that wavelength is based on frequency. Suppose that I am using 77 GHz to 81 GHz frequency range for AWR1642BOOST. Please advise which values of frequency should I use for calculating the wavelength ? Will I get optimally good approximate results if I use a single value OR not ? If yes, then in such case should I use 77 GHz, or 81 GHz or 79 GHz (mean of 77 and 81 GHz) ?
7- The previous post advises : " A convenient way to do this is to have a stationary scenario and use the signal level in the non-zero doppler bins as a measure of the noise floor. "
In an attempt to act on the above advice, I have carried out the following steps:
a) By using MATLAB, from raw ADC data mentioned in para 1 above, I extracted a column vector corresponding to a single chirp on a single receiver (a single chirp being used as a prototype step, I will use more chirp later on). I used fft function of MATLAB to obtain the fft of data. I then converted sample index to frequency and I plotted this frequency against Power Spectral Density (PSD). The PSD values are obtained by the formula PSD = abs(rawfft).^2/nfft, which explains that, for each frequency bin/step, I am squaring the magnitude of each complex number and then dividing it by the length of fft.
b) What do non-zero doppler bins mean / signify in the advice from previous post ? If it is going to be a stationary scenario as advised by TI, then virtually there will NOT be any non-zero doppler bins as there will be virtually no motion observed. I have not taken yet the 2nd fft for doppler estimation, however, I feel that as I have a stationary scenario, I will will have virtually no bin with a doppler level. In such scenario, I feel that the PSD values (after excluding one target peak) could be assumed as noise floor and could be taken as SNR values.
c) I have a single target case. Therefore, I obtained the PSD value of the single peak corresponding to the target. After that, I took sum of all the PSD values for the whole fft length and then I subtracted PSD value of one dominant peak from that sum. After that, I took average of the remaining (nfft-1) values.
Now as the PSD value of the target peak has been removed, I assume that the PSD values of remaining (nfft-1) correspond to the noise floor and I take them as SNR. As I mentioned above, I took their average and I am using it as SNR and using it in the above SNR equation. Is my supposition of using PSD as SNR right or not ?
d) I am then using the above equation with the above obtained SNR value and calculating the target RCS. Does my procedure seem ok ?
Thanking you in advance and regards.