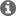Hi,
I watched the TI tutorials on velocity calculations and following are the two key formulas I use:
1 - Maximum velocity ( V(m) ) = L / (4Tc) where L is the wavelength and Tc is the chirp period in a given frame
2 - Velocity resolution ( V(r) ) = L / (2Tf) where L is the wavelength and Tf is the frame period.
I am trying to calculate V(m) and V(r) for the "People Tracking and Counting" configuration file provided for IWR6843ISK as shown below (i.e. see underlined parameters I am interested in)
I studied the frame structure for the above example and following figure summarizes my understanding. There are two different chirps defined for each frame (i.e. indicated with black and red below) These chirps are based on the same profile ID and the only difference is each chirp type is transmitted using different antennas. According to the chirp period, Tc, (which I highlighted in the TI chirp reference figure further below) each red and black chirps have a duration of 92 us as shown. The total active time (Ta) where chirps are transmitted can be calculated as 256 x 92 us = 23.552 ms. Given that Tf = 50 ms, the gap at the end of each frame (Tg) is automatically calculated (by the mmWave Studio) as 26.448 ms (i.e. 50 ms - 23.552 ms = 26.448 ms) Therefore, the duty cycle of each frame is Ta/Tf = 47.1% (i.e. just below 50%)
Next, I will walk you through my calculations for V(r) and V(m) here and request your help on where I seem to be making a mistake.
The starting frequency is specified as 60.6 GHz and therefore the wavelength (L) is 4.95 mm in this example.
1 - My V(r) calculation:
According to the reference formula V(r) = L / (2Tf), I plug in L=4.95e-3 and the Tf = 50 ms (from the above frame structure).
Therefore, V(r) = 0.0495 m/sec = 0.178 km/hr
According to the table I shared above, V(r) is supposed to be 0.36 km/hr, which is almost twice as what I am calculating. The first thing that comes to mind is the duty cycle (which is almost 50%), which is not factored in my calculation. Therefore, it seems I should be factoring that in as:
V(r) = 0.178 / (47.1%) = 0.378 km/hr , which is close to the listed result above.
I am not sure if the duty cycle is the reason why my first calculation is off, and also whether it should be factored in as highlighted above.
2 - My V(m) calculation:
According to the reference formula V(m) = L / (4Tc), I plug in L=4.95e-3 and the Tc = 92 us (as per the above frame structure).
V(m) = 13.451 m/sec (i.e. 48.42 km/hr)
My V(m) seems to be almost twice as large as the listed result in the table above, and I think this is attributed to the duty cycle again. (As my calculation implicitly assumes transmitting chirps for the entire duration of the frame, which is actually not the case!)
Therefore, my intuition tells me I should factor in the duty cycle at the end as follows to get the correct answer:
V(m) = 48.42 * (47.1%) = 22.8 km/hr, which is closer to the listed result in the table above.
Could you please shed light onto the duty cycle aspect and any other term I might be missing in my V(r) and V(m) calculations I listed above? I presume in more complicated frame and chirp configurations (with different Tc values for example), calculation of V(r) and V(m) are also going to have to vary. However, if I get an understanding of this particular case, I think I can generalize it to other cases.
Thank you for your help.
Regards,
Cagri