アナログ/デジタル・コンバータ(ADC)を評価する際に、多くの設計者がADCのダイナミック特性を解析するために高速フーリエ変換(FFT)法を使用しています。このダイナミック特性テスト手法は、ADCの入力側に純シングルトーン正弦波信号を加え、ADCデータの周波数領域解析を行い、スペクトルに含まれるノイズと歪み成分を数量化します。ADCの特性を調べる際にコヒーレント・サンプリングを用いると、FFTのスペクトル成分を正確に分解することができます。コヒーレント・サンプリング基準に対応できないアプリケーションの場合、サンプリングしたデータにウィンドウ加重関数を適用してスペクトル漏れを最小化します。
本稿では、ADCのFFT解析に関する2つの重要なコンセプト、すなわちADC評価の際のコヒーレント・サンプリングの基礎と非コヒーレント・サンプリングの影響を考察します。さらに、今後のブログで、コヒーレント・サンプリング、ウィンドウ・サンプリング、最適なウィンドウ選択のための基準について取り上げます。
 図1:18ビット、1MSPS、真の差動入力SAR ADC「ADS 8881」のFFTスペクトル
図1:18ビット、1MSPS、真の差動入力SAR ADC「ADS 8881」のFFTスペクトル
FFTは、サンプリングした時間領域信号の離散フーリエ変換(DFT)を行うための効率的なアルゴリズムです。この手法は、2の冪であるM個のサンプルを含む時間領域レコードを必要とします。FFTスペクトルは、DCからfS/2までの範囲のM/2個の離散周波数ビンおよび周波数分解能fS/Mで構成されており、その際にfSはサンプリング周波数です。図1は逐次比較型(SAR)ADCであるADS 8881を評価するFFTスペクトルの例です。
重要なのは、ADCを最終アプリケーションと類似の条件で評価することです。例えば、ADCは自動制御、センサ、通信、高速計装機器、オーディオなどのいくつかの分野でACやダイナミックに変化する信号を測定します。FFTの出力スペクトルを観察する場合、デジタル化信号のさまざまな高調波/ノイズ成分の大きさを測定することにより、ADCのダイナミック応答の数量化が容易になります。システム・エンジニアは、デバイスのダイナミック特性を比較するために、さまざまな仕様を参照します。例えば、信号対ノイズ比(SNR)は、アナログ/デジタル変換プロセスによって信号に挿入されたノイズとスプリアス成分の量を測定したものです。式1に示すように、SNRは搬送波との関係において、スペクトル中の基本トーン信号出力の、ノイズ出力に対する比(DCと高調波を除く)として求められます。
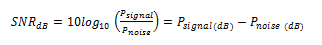 同様に、式2に示すように、全高調波歪み(THD)は、高調波(一般には最初の9つの高調波)出力の、基本信号出力に対する比です。
同様に、式2に示すように、全高調波歪み(THD)は、高調波(一般には最初の9つの高調波)出力の、基本信号出力に対する比です。
 ベンチで高精度ADCの評価を行う際には、テストのために低歪みの高精度信号源が必要です。アナログ/デジタル変換プロセスで生じる非常に小さなノイズ/歪み成分を分解するために、正弦波入力信号はテスト時のADCよりも数段優れたスペクトル特性が必要です。ADCの性能よりも、少なくとも10dBほど高い信号源であれば問題ありませ���。多くの場合、関数発生器のスペクトル純度は十分ではなく、図2に示すように、テスト信号のノイズと歪みを低減するために関数発生器とADCの���に高次のバンドパス・フィルタが必要となります。
ベンチで高精度ADCの評価を行う際には、テストのために低歪みの高精度信号源が必要です。アナログ/デジタル変換プロセスで生じる非常に小さなノイズ/歪み成分を分解するために、正弦波入力信号はテスト時のADCよりも数段優れたスペクトル特性が必要です。ADCの性能よりも、少なくとも10dBほど高い信号源であれば問題ありませ���。多くの場合、関数発生器のスペクトル純度は十分ではなく、図2に示すように、テスト信号のノイズと歪みを低減するために関数発生器とADCの���に高次のバンドパス・フィルタが必要となります。
図2:ダイナミックSAR ADC評価のための標準的なベンチテスト設定
テスト信号の純度に加えて、FFT解析では入力信号周波数が重要な役割を果たします。FFTでは、入力信号周波数、サンプリング周波数、サンプル数の間に関係が存在します。それにより、コヒーレント・サンプリングというコンセプトが生まれます。
連続フーリエ変換(CFT)では、無限の時間間隔から信号を積分します。それに対し、FFT はCFTの近似であり、有限の時間間隔中にサンプリングされたデータ・レコードを変換します。FFTを、無限シーケンスがサンプリング・データの無限回にわたる複製により形成されるCFTのサンプル版と考えてください。それを示したのが図3で、データ・レコード・フレームに含まれる信号が反復されています。
 図3:整数個の正弦波サイクルを含むタイム・レコードとFFT周波数スペクトル
図3:整数個の正弦波サイクルを含むタイム・レコードとFFT周波数スペクトル
図3(上段)はコヒーレント・サンプリングを使用した際の、タイム・データ・レコード・フレーム内に含まれる整数個の正弦波サイクルです。データ・レコードの終端で不連続性が発生しないことから、結果的に得られるFFTは正弦波信号の適切な周波数スペクトルを示します(下段)。
時間領域フレーム内で同じ値でタイム・レコードのサンプルの開始と終止が行われない場合、FFTはそれを波形の不連続と解釈します。それでは、サンプリングしたデータ・レコードが非整数個のサイクルを含むケースについて検討してみます(図4)。
図4:非整数個のサイクルを持つデータ・レコードは周波数領域でスペクトル漏れを発生
図4は、タイム・レコード内で非整数個のサイクルを持つ正弦波信号のFFTを示します。サンプリングしたレコードの終端で発生する急激な遷移は、元の正弦波信号に存在しない周波数成分をFFTで生成します。FFTで1つの周波数ビン内に含まれるべきだった正弦波信号エネルギーは、他の周波数ビンにも波及します。FFT内の他の周波数ビンへの波及効果は、スペクトル漏れと呼ばれています。
周期的波形のコヒーレント・サンプリングは、周期的入力信号の整数個数のサイクルがサンプリング・データ・フレームに含まれている際に実現できます。コヒーレント・サンプリングを使用する場合、結果的に得られるFFTが示すのは入力とその高調波に相当する周波数だけです。
次回、シリーズの2回目では、ベンチ上でコヒーレント・サンプリングを実現するために必要な基準について説明します。
その他のリソース:
- ADS 8881のデータシート
- Bores Signal Processing「FFT Window Functions: Limits on FFT Analysis」
- 「高精度ADCを評価する際の正しいFFTウィンドウ機能の選択法」(英語)Chioye, Luis 著、Electronic Design、2013年11月12日
- 歪みとノイズを最小化するために最適化された18ビット1Mspsデータ・アクイジション・リファレンス・デザイン(TIPD 115)
上記の記事は下記 URL より翻訳転載されました。
*ご質問は E2E 日本語コミュニティにお願い致します。


