Dave Wilson(デーブ・ウィルソン)、モーター製品エバンジェリスト、テキサス・インスツルメンツ
Richard Poley(リチャード・ポーリー)は、TI の C2000 マイコン(MCU)トレーニングマネージャで、TI Industrial Control Seminar(産業用制御セミナー)シリーズの講師も務めています。 (制御理論に関する Richard のクラスは非常に楽しいので、ぜひ参加してください。) Richard が好んで話す説明の中に、PI(D)コントローラがどのようないきさつで考案されたか、というものがあります。 ロシア系米国人の Nicolas Minorsky(ニコラス・ミノルスキー)は 1920 年代前半に米国海軍向けに自動操舵システムを設計していました。さまざまな条件下で、操舵手がどのような方法で操船するかを観察していました。 Wikipedia.org によると、平穏な条件下では、誤差信号の簡潔な増幅で操舵手の動作を近似できる可能性があることに Nicolas は気付きました。ただし、固定的な方向に吹く強い風など、固定的な変動が発生している場合は、この簡潔なモデルは不適切でした。 最終的に、連続的な固定状態の誤差を表す補正として、1 つの積分項を追加する結果になりました。 後に、制御しやすさを改善するために、微分項(Derivative term)も追加されました。
Wikipedia.org の説明の参照を続けると、PI コントローラに基づく自動操船システムの試験的試行は、戦艦ニューメキシコで実施されました。 いくつか調整を加えた後、Nicolas は角度誤差を 2 度未満に制御することができました。 D 項を追加した時点で、誤差はさらに改善されて 1/6 度以内になりましたが、これは大半の操舵手が手動で達成できる誤差より良好なものでした。 Nicolas Minorsky はこの発見(同じく 1920 年代前半)を刊行しましたが、多くの有名な発明家の場合と同様、この時点でこの内容を意識したのはごく少数のエンジニアのみでした。 一方、現代に生きる私たちは、Nicolas の発見が制御システムの設計に新時代をもたらしたことを知っています。
戦艦 ニューメキシコは当時、PID 制御を後付けするために変更を加えられた
TI の Industrial Control(産業用制御)セミナーで筆者が毎回のように尋ねられる質問は、「PI コントローラを調整するとしたら、どのような手段を使用しますか」というものです。 私は通常、ボード線図に手を加えるか、何らかのシミュレーション・データを画面に映し出し、このプロセスがある程度経験的であり、また注目しているある種の応答に対する非常に主観的な手法であることを示しています。 このように答えるとたいていの場合は、聴衆は当てが外れたような顔で筆者の顔を眺める結果になります。聴衆は、筆者が質問に答える代わりに、質問をかわしたことを理解するからです。
最近開催した 1 回のセミナーが終わった後、もっと的確に回答する必要があると判断しました。そのため、このトピックをもっと真剣に調査する作業を開始しました。 新しく気付いた事実により、筆者は PI コントローラに関する考え方を改めました。 現在では、PI 制御ループ(速度ループであるか電流ループにであるかにかかわりなく)の設計と調整は、筆者が以前考えていたものより確定的(Deterministic)であると確信しています。 注目している応答の種類によっては依然として高い自由度が存在していること、または PI の基礎的な構造自体に、名状しがたい変動に関する終わりのない長い説明が含まれていること明らかです。 一方で、いくつかの基本的なルールに従うと、博士号がなくても PI ループを調整することはできます。
最初に、小さい要点を押さえておきましょう。 筆者が実施した分析は、実際の極が複数存在する負荷に限定されています。 モーターと負荷の間に存在する過度にねじれた共振の結果として、顕著で複雑な複数の極を持つ設計を取り扱っている場合は、いずれにしても共振の効果を打ち消すために、コントローラを簡潔な PI 構造より洗練されたものにする必要があります。 ただし大部分の状況では、固定的なシャフト・カプラが、ねじれた共振に対処し、標準的な PI 制御構造の使用が受け入れ可能な水準まで抑制されます。 また、このブログ・シリーズの大半を通じて、粘性減衰が負荷に存在していないことを筆者は想定します。
さて、「PI コントローラ」という言い回しを耳にしたときに、皆様はどのようなことを連想しますか。 多くの人にとっては、以下に示すような従来型の並列パス・トポロジーを意味します。 誤差信号は 2 つの個別のパスへと分割されます。1 つは直接増幅され、もう 1 つは増幅後、積分されます。 増幅された誤差信号と積分された誤差信号は、出力の地点で単純な加算操作により再結合されます。 積分器を含めているのは、システムの安定状態での誤差を 0 に誘導するためです。安定状態での誤差が 0 以外である場合は理論的に、無制限の積分器出力という結果をもたらします。 積分器は PI コントローラの動作で重要な役割を演じますが、頭が痛くなるような多くの問題も招き入れます。 たとえば、制御ループ内の誤差が 0 であったとしましょう。この値は、制御された信号が、指令された信号に等しいことを意味します。 ここで、制御された信号に対して小さいオフセットを追加し、何が起こるかを観察しましょう。 誤差信号はもう 0 ではないので、誤差信号を再び 0 にしようとする試行の過程で、積分器の出力は時間の経過に従って大きくなります。
ここで、オフセットを取り除き、何が起こるかを観察しましょう。 制御された信号は徐々に、再び指令された値へと戻り始めますが、ただちに戻るわけではありません。 積分器の出力は依然として非常に大きいので、積分器の出力が「減衰」している間、制御された信号は指令された値を大幅にオーバーシュートする結果になります。 この期間にわたって、「制御された」信号のプロファイルはまったく制御されていません。さらに、信号に対して制約が加えられない場合は、システムを損傷させる結果になるおそれもあります。 これは、ばねを強く押し縮めた(wind up)後、突然にばねを解放することに似ています。 この理由で、PI コントローラにおけるこの効果を「ワインドアップ」(仕上げ)と呼びます。 このワインドアップ効果を緩和する方法は多数存在しますが、ほとんどの技法には何らかの種類で積分器の出力を制限することが関係しています。 このシリーズでは後ほど、この点について詳細に説明する予定です。
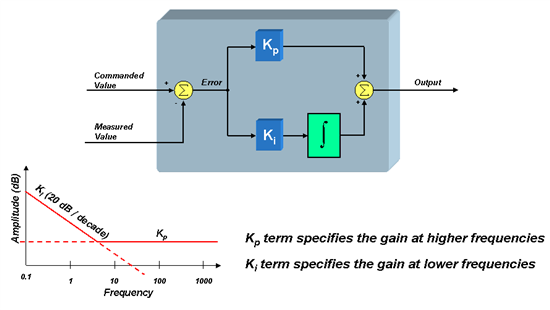
PI トポロジーを理解するのはかなり容易ですが、「Kp と Ki の値をどのように設定しますか」という質問に関しては、深遠な秘密があります。 これは、より詳細に説明する必要のある主題ですが、各項がモーター制御システムに及ぼす影響を直感的に理解するのは困難です。 Kp 項は、上の図に示したように、制御ループの高周波ゲインを設定します。 Ki 項は低周波ゲインを設定し、理論的には DC のときに無限のゲインを達成します。 高周波と低周波を区分する周波数を、コントローラの「ゼロ」(導関数の値が 0 になる)と呼んでおり、周波数プロットにおける変曲点に対応します。 ただし、現時点ではコントローラの複数の係数を設定する方法を詳細に理解できる段階までは進んでいません。 そのため、大半のエンジニアは単純に「当たりか外れか」という、当てになる値を試行錯誤で見つける方法に頼っています。
PI コントローラに関するもう 1 つの人気のある形式(および筆者が今後の分析で使用することを予定している形式)は、以下に示す「直列」トポロジーです。
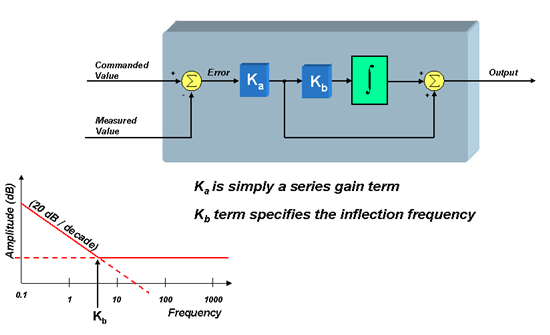
この図からは、2 セットの係数の間にある関係が次のように定義されることを理解できます。
ただし、この構造では Ka がすべての周波数におけるゲインを設定し、Kb は rad/sec(ラジアン/秒)単位でのコントローラの変曲点(ゼロ)を直接的に定義していることを理解できます。 どちらの形式も、ソフトウェア実装の観点ではかなりよく似ています。 ただし、多くのエンジニアは並列形式より直列形式を好んでいます。Ka と Kb が現実のシステム・パラメータに直接的に相関しているからです。 Ka がコントローラの性能に及ぼす影響はかなり容易に理解できます。この係数は開ループ伝達関数内のゲインを設定するからです。 ところで、ゼロつまり変曲点はシステムにとってどれほど重要なものですか。 これは筆者が発見した事実の 1 つですが、詳細については次回のブログでお知らせしたいと思います。 それまでの間、モーターを引き続き回転させてください。
上記の記事は下記 URL より翻訳転載されました。
*ご質問は E2E 日本語コミュニティにお願い致します。