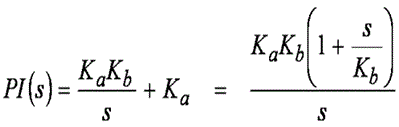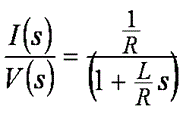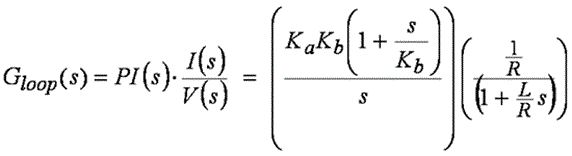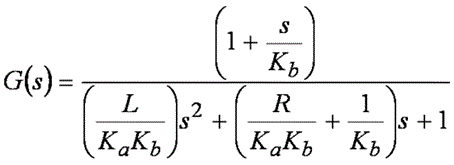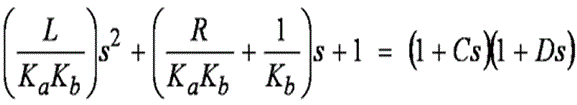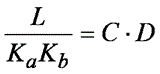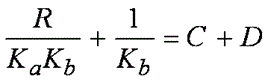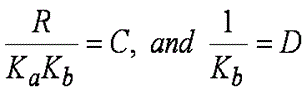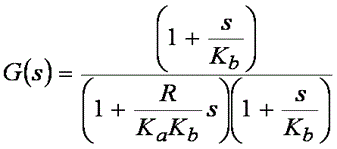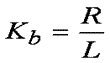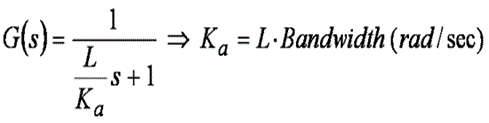Dave Wilson(デーブ・ウィルソン)、モーター製品エバンジェリスト、テキサス・インスツルメンツ
このトピックに関する筆者の前回のブログでは、PI コントローラのいきさつを簡単に振り返り、現在一般的に使用されている 2 つの形式を示しました。 皆様がどちらの形式を使用するかにかかわりなく、周波数応答は同一です。 ただしこのシリーズの分析では、次に示すように、PI コントローラの直列形式に注目します。

制御システムの周波数安定性分析を実施したことがある場合は、Ka が非常に重要な理由を理解していることでしょう。この係数は PI 制御ループのゲインを設定し、その結果、システムの安定性に関して顕著な効果をもたらすからです。 ただし、グラフでは変曲点(導関数の値が 0 になる「ゼロ」周波数)として表現されるとともに、システムの性能にとって重要な、しかし名状しがたい役割も演じます。 この係数を理解するには、PI コントローラに対応する伝達関数を導くために、数学の領域にある程度立ち入る(あまり深入りしないように注意します)必要があります。また、コントローラの「ゼロ」が、全体的なシステム応答にとってどのような役割を演じるかも理解する必要があります。 誤差信号からコントローラの出力に対する変換を行う、「s 領域」伝達関数を次のように定義することができます。
式 1
この式からは、s = 0 の地点に極が存在すること、また s = Kb(rad/sec、ラジアン/秒)の地点にゼロが存在することを明確に理解できます。 では、このゼロの値(導関数が 0 になる周波数)が非常に重要なのはなぜでしょうか。 この質問に答えるために、次の図のように、モーターを制御する電流モーター・コントローラの中心部に PI コントローラを投入してみましょう。
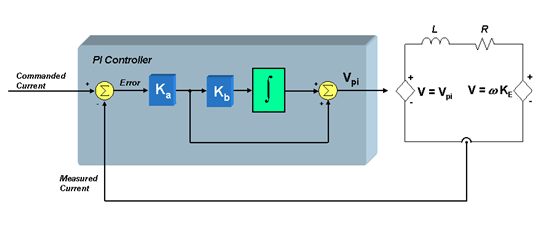
モーターの巻線に関して 1 次近似を使用し、1 個の抵抗、1 個のインダクタ、および逆起電力の電圧生成源からなる簡潔な直列回路を想定します。 逆起電力が各時点で一定である(通常は電流を基準とすると、それより緩やかに変化するため)と仮定すると、モーター電圧からモーター電流への変換を行う小信号伝達関数を次のように定義できます。
式 2
さらに、バス電圧と PWM ゲインのスケーリングが Ka 項に含まれていると仮定する場合は、「ループ・ゲイン」を、PI コントローラの伝達関数と、上記 RL 回路の V-to-I (電圧から電流への変換)伝達関数の積として定義できます。
式 3
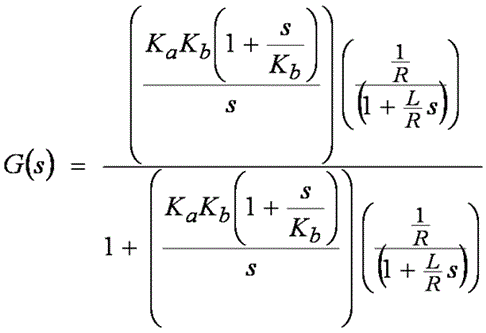
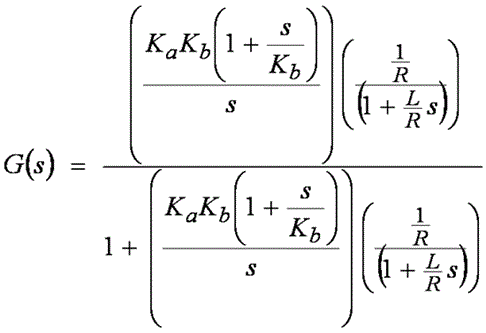
システム全体の応答(閉ループ・ゲイン)を見つけるには、おそらく学部レベルの制御システム・クラスで見かけたことがあると思われる次の式を使用する必要があります。
この式では、フィードバック・ゲイン H(s) = 1 と仮定しています。 式 4
式 3 を式 4 に代入すると、次の式が得られます。
式 5
式が簡単になるどころか、複雑になってしまいました。今はこの点に目をつぶってください。 代数学の観点では少々乱暴なところもあるのですが、この式を次のように単純化することができます。
式 6
分母は「s」に関する 2 次方程式です。これは、伝達関数に 2 つの極が存在することを意味します。 Ka と Kb を選択する方法に十分な注意を払わない場合は、複素数の極(扱いに困ります)という結果に容易に迷い込むおそれがあります。 このような複素数の極と jw 軸との距離によっては、実際のシステムは本当に頭が痛くなるような複数の共振ピークを持つおそれもあります。 そのため、今この場では、複素数の極を避ける方法で Ka と Kb を選択するという方針を想定します。 言い換えると、分母を次のように因数分解した形式に変換することができます。
式 7
ここで、C と D は実数です。
式の右辺を展開し、展開結果を式の左辺と比較すると、実数の極を得るには次の条件を満たす必要があることがわかります。
式 8
および
式 9
式 8 と 9 を解くための最初の試みとして、式 9 の両辺にある 2 つの項がそれぞれ等しいと単純化してみましょう(訳注:式 10 の仮定は、A+B = C+D という式で根拠を明示せずに A = C、B = D と仮定していることになります。式 12 もそこから導かれています。この仮定は簡略化を目的としていますが、R と L を測定し、Ka と Kb の妥当性を実験で確認することをお勧めします)。 つまり、
式 10
筆者がこのような代入を推奨する理由は、明確化を推進するためです。 式 6 の分母を、式 7 のように因数分解の形式で表現した等価物で置き換え、その後、式 10 で推奨した代入を行うと、次の式が得られます。
式 11
この式を眺めると、興味深い事実に気が付きませんか。 「D」を代入した結果、閉ループ・ゲインの式内に存在していたゼロを打ち消す極が得られました。 C と D を正しく選択すると、実数の極を得ることに加えて、ただ 1 つの実数の極を持ち、ゼロを持たない閉ループ・システム応答を作り出すことができます。 先鋭な周波数応答や共振条件は存在しません。 見事な 1 極ローパス・ロールオフ応答です。
ただし、ちょっと待ってください。ほかにも注意すべき点があります。 (このように話すと、安っぽい情報コマーシャルのアナウンサーになった気分です。) C と D に関して式 10 で推奨した代入を、式 8 に適用すると、次の等式が得られます。
式 12
Kb が、コントローラのゼロ(変曲点)が発生する周波数であることを思い出してください。 式 11 で説明した応答を得るために必要な作業は、Kb(コントローラのゼロ周波数)を、制御対象プラントの極に等しい値に設定することのみです。
ここまでで、Kb を設定する方法はわかりました。Ka はどうでしょうか。 閉ループ・システムの応答 G(s) を書き直し、ここまでに説明したすべての代入を行ってみましょう。次の式が得られます。
式 13
つまり、Ka は、モーターのインダクタンスによってスケール化される、制御システムの帯域幅を直接設定することがわかります。 数値の上では、Ka は帯域幅のカットオフ周波数に達した時点での誘導性インピーダンスに等しくなります。
要約すると、どのような結論が得られたでしょうか。 一部の数式が理解できなかった場合でも、電流ループの PI コントローラを設計する際に使用できるいくつかの簡潔なルールがあります。
1. Kb は PI コントローラのゼロを設定します。 伝達関数(つまりモーター内の電流)でただ 1 つの実数の極を持つように、プラント・パラメータを制御するには、Kb をこの極と同じ値に設定します。 このような値に設定すると、極/ゼロの打ち消しが生じる結果になり、実数の極を 1 つだけ持つ閉ループ応答が作成されることになります。 PI コントローラは、より大きい制御ループの一部であり、Kb は外部から認識できるものではありません。Kb は、PI 制御ループ自体の中で、極とゼロの打ち消しの目的でのみ使用するものだからです。
2. Ka は、閉ループ・システム応答の帯域幅を設定します。 式 13 で示したように、Ka の値が大きくなると、電流ループ帯域幅も大きくなります。 適切な帯域幅の選択方法については、今後投稿するブログで説明する予定です。
ああ、筆者は今回のブログ投稿 1 回で脳をかなり酷使しました。 今回の投稿は少々「数学の説明が多すぎた」と感じています。できれば、皆様がこれらの式を理解できたことを願っています。 より重要なこととして、PI 電流制御ループを設計する方法に関して、これらの式が何を伝えようとしていたのか、皆様が理解されたことを願っています。 筆者の次回ブログ投稿では、PI 電流コントローラを内蔵した、カスケード型の PI 速度ループを設計する方法について説明したいと思います。 それまでの間、
モーターを引き続き回転させてください。
上記の記事は下記 URL より翻訳転載されました。
*ご質問は E2E 日本語コミュニティにお願い致します。