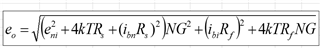Other Parts Discussed in Thread: THS3062, , OPA695
I'm looking at using the THS3061 op-amp (and by extension, possibly the THS3062 op-amp) as part of a simple circuit to add and subtract voltages. These voltages are small-signal voltages (with amplitudes of 100 mV or lower and a bandwidth of 200 MHz). I wanted to use the THS3061 op-amp because of its high bandwidth as well as how current-feedback amplifier feedback is dependent on the feedback resistor. I figured that as a current-feedback amplifier, the wide bandwidth range will be beneficial in my application, not to mention how it isn't determined by the gain-bandwidth product as with a voltage-feedback op-amp.
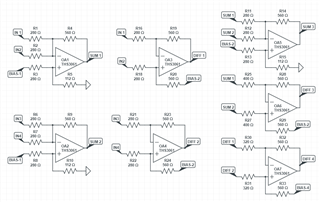
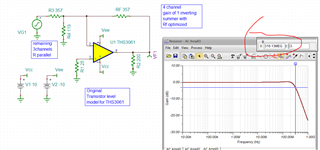
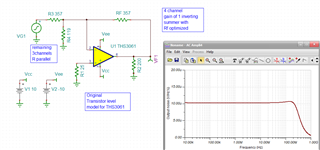
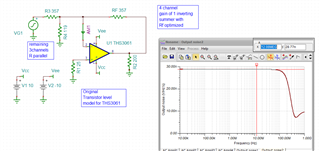
Below is an image showing how I plan to use the THS3061, adding voltages on the left circuit and subtracting voltages on the right circuit. It's a pretty simple circuit, and this is just a simplified application to make things easy to understand, but my question is with the feedback resistor values. According to the datasheet, it lists recommended feedback resistor values. Now, my application requires the gain to be between -2 and 2 for simplicity's sake. The gain may vary between these values, but through simulations, it shouldn't exceed an absolute gain of 2 for each op-amp circuit (so, one op-amp may have a gain of -2 whereas another may have a gain of 1.75). With that limitation, the recommended feedback/gain value section in the datasheets mentions that the bandwidth is inversely proportional to the feedback resistor. As gain increases, it appears that the feedback resistor is reduced accordingly. In order to keep a high bandwidth given my gain requirement, is it best to keep FB-1 and FB-2 to a fixed value (closest value I see here is 560) and adjust the RG-1/RG-2 resistor values to achieve the gains I need?
If it helps, the op-amp circuits will be cascaded together, though it doesn't show in this simplified example. For example, OUT1 may go into the second circuit as IN3. Circuit 1 may have a gain of -2 while circuit 2 may have a gain of -2. This is just a rough example, but I hope it gets the point across.