When creating a power budget in an electrical design, it’s important to know how much power can be consumed by every device in the design. Current sensors have several power consumption components, some higher than others, that should be accounted for. As an example, the INA190 will be used throughout, showing the key parameters from the datasheet to be used in order to calculate the current sense amplifier’s total potential power consumption.
Quiescent current (Iq)
The first component, and easiest to calculate, is power from the device’s quiescent current. This power component is dependent on both the Iq of the device as well as the supply voltage (Vs). Looking at the Iq of the INA190 from the datasheet, we see the maximum Iq at room temperature is 65 uA, and 90 uA over temperature (maximum instead of typical values should be used when calculating power to plan for highest case scenarios), and the specified operating condition for Vs at 5 V.
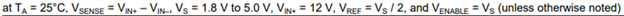

As power is defined by P = I * V, the highest power dissipation for the INA190 from the combination of Iq and Vs would be
P = 65 uA * 5 V
P(Iq) = 325 uW (at 25°C)
- or -
P = 90 uA * 5 V
P(Iq) = 450 uW (over temperature)
These power estimates can be calculated more accurately if the system’s maximum Vs is known and used in the calculations rather than the datasheet’s specified operating Vs of 5 V.
Load current (Iout)
The second power component comes from the output, and can come from either sourcing or sinking current (for this example we will focus on sourcing current). This power component is derived from the combination of the output voltage and current required from the device, and can be calculated with the equation (Vs - Vout) * Iout. When designing for worst-case, maximum power occurs when Vout = Vs / 2 (see this TIPL video for further explanation of this concept)
Continuing our example using a Vs of 5 V, maximum output power occurs when Vout = 2.5 V. Assuming a 10 kΩ load connected to the output, Iout would be 2.5 V / 10 kΩ = 0.25 mA. Calculating the power in this condition becomes
P = 2.5 V * 0.25 mA
P(Iout) = 625 uW (at 25°C)
Common mode current (Ib)
Finally, the third power component in the power budget analysis comes from the common-mode current. This power comes from the combination of the common-mode voltage (Vcm) and the input bias current (Ib) flowing into the input pins of the device, and is calculated with the equation Vcm * Ib * 2. The * 2 multiplier is due to the Ib being essentially equal and flowing into each input pin.
From the specification table of the INA190 datasheet, Ib is specified to be a maximum of 3 nA at a Vcm of 12 V.
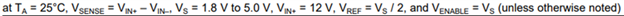

Using these values to calculate the Ib power component, we get
P = 12 V * 3 nA * 2
P(Ib) = 72 nW (at 25°C)
If the system will be using a Vcm outside of the specified condition like the above example, check the device’s data sheet. Generally, there is additional data in the figures below the specification table that includes Ib vs. Vcm (for the INA190, this is figure 14), that. However, there is a caveat here in that these curves are typically created using typical values rather than maximum values, and this should be accounted for.
Enable current (Ien)
Devices like the INA190 have the added functionality of enable / disable, and this function comes with some additional power consumption that should be accounted for. Looking at the datasheet, the maximum leakage current into the enable pin is specified to be 100 nA.

Again, with a Vs of 5 V, and using Vs as the enable voltage level, calculating the enable current power becomes
P = 5 V * 100 nA
P(Ien) = 500 nW
Total power (Ptot)
Now that each of the power consumption components have been calculated, they can simply be summed to find the total power consumption of the device as a whole.
P(tot) = P(Iq) + P(Iout) + P(Ib) + P(Ien)
P(tot) = 325 uW + 625 uW + 72 nW + 500 nW
P(tot) = 950.572 uW
- or -
~ 951 uW
Calculating the total power consumption of a current sensing amplifier is necessary when creating a total system power budget. Using the above example as a guideline, the calculations can be replicated by replacing the values in the example with real world system maximum values, especially for Vs, Vout, and Iout.

