Other Parts Discussed in Thread: OPA134
I wached the TI Precsion Lab.
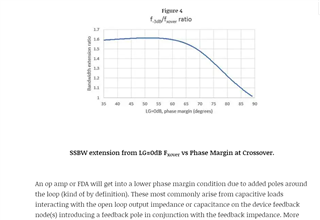
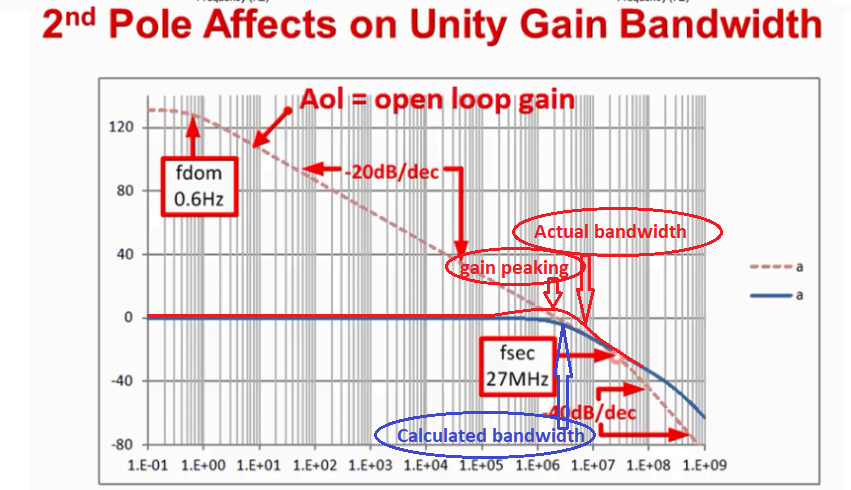
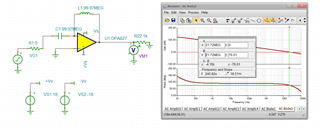
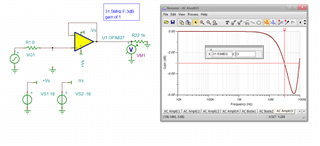
For calculation, the bandwidth is 11MHZ. For simulation, it is 18MHZ.
I want to confirm I use 11MHZ or 18MHZ as the bandwidth when I design the circuit? Which is correct? Why?
If use 18MHZ as the bandwidth when I design the circuit, this mean I need to simulate to confirm the bandwidth at the first when I design the circuit?

Tengfei