Other Parts Discussed in Thread: TINA-TI, , INA326
Hi,
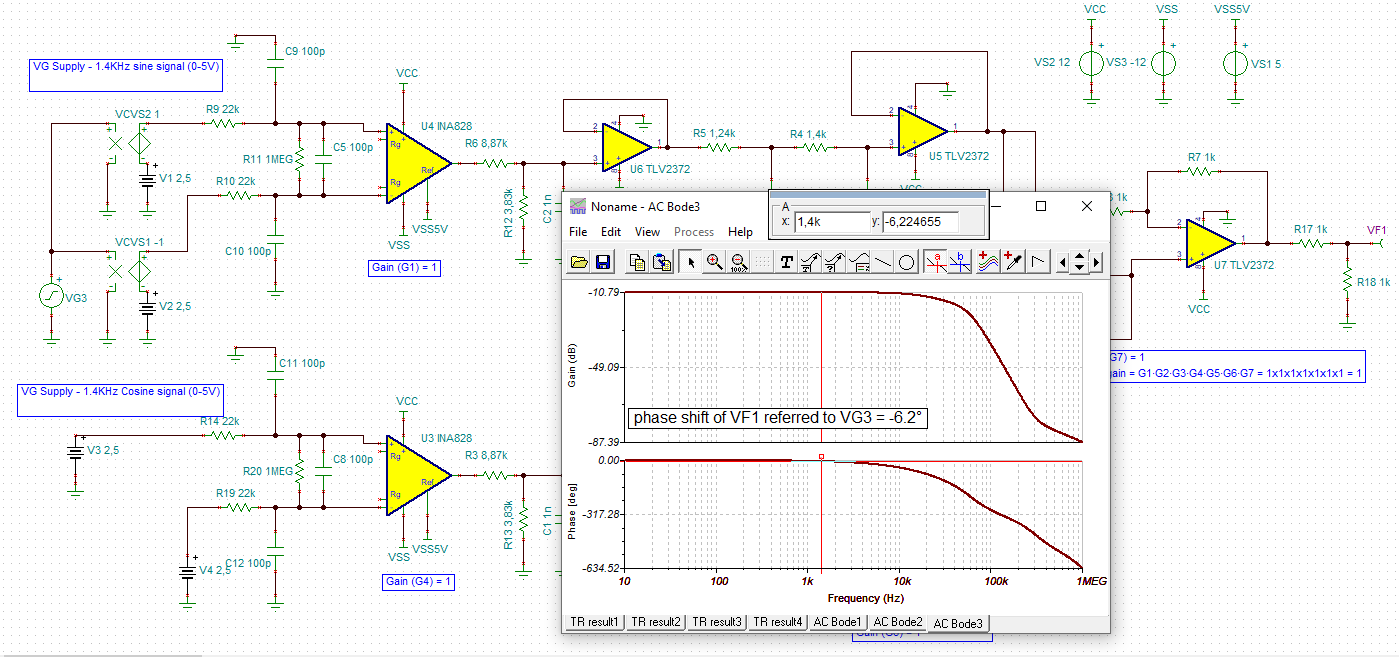
- The below attached circuit converts the differential sine and cosine signals to single ended signal, it is then filtered using a 3rd order low pass filter, finally the filtered cos and sine signals are summed and sent to the ADC of TMS320F28377DPTPEP (ADC voltage range is 0V to 3V) controller.
- How to design the input filtering circuit for the IC INA828ID (common mode filter and differential mode filter)?
- Considering the circuit attached below how to theoretically calculate the phase shift of the circuit (Phase shift calculated between the input (COS+SINE) and output (COS+SINE))?
- Input to the circuit (INA828ID) is differential sine and cosine signals of 1.4k Hz (0V - 5V).
- The 3rd order LPF circuit has cutoff frequency of 60K Hz.
Thank you.