Other Parts Discussed in Thread: TINA-TI
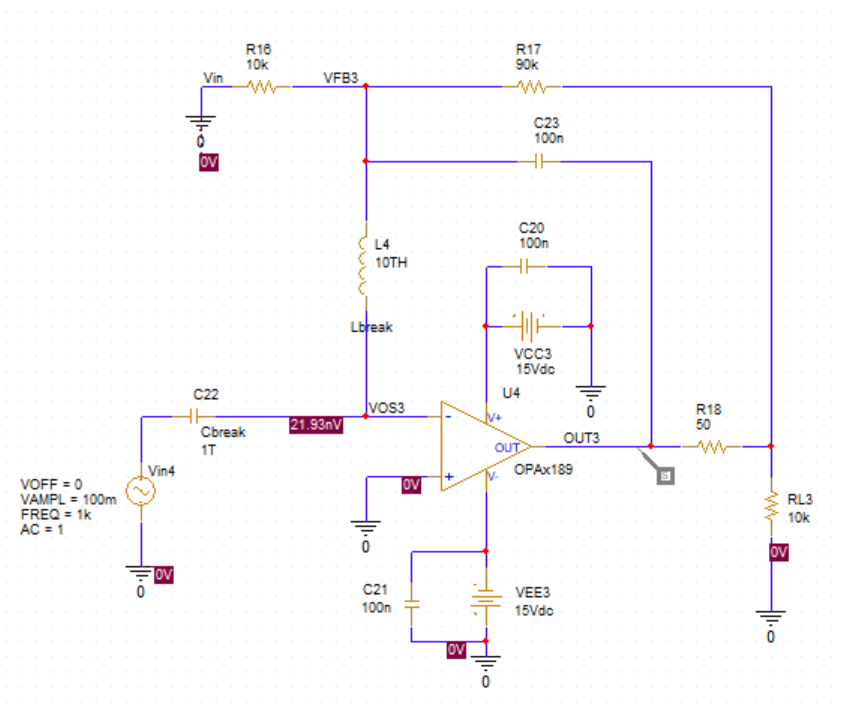
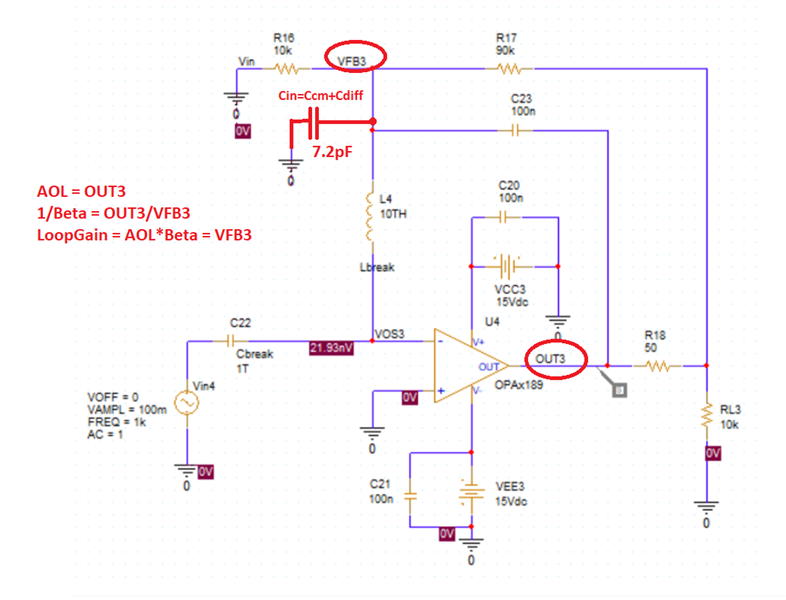
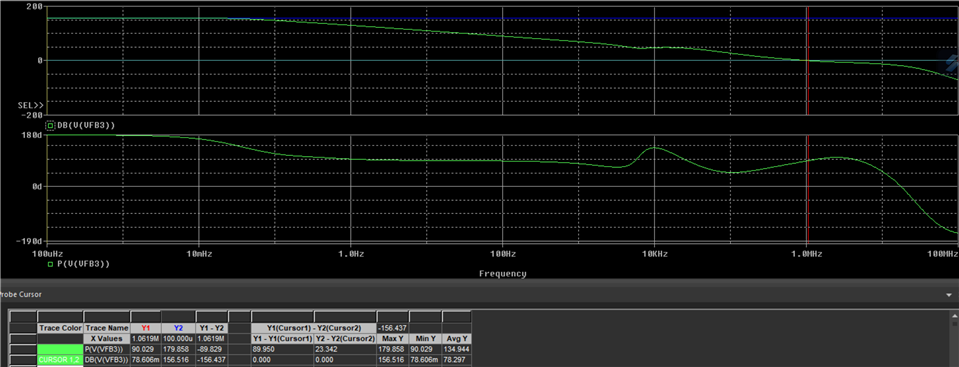
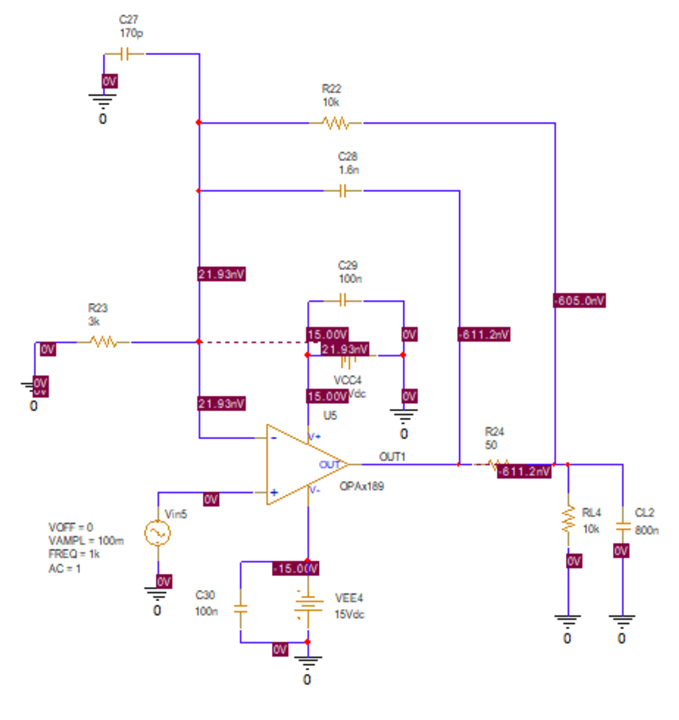
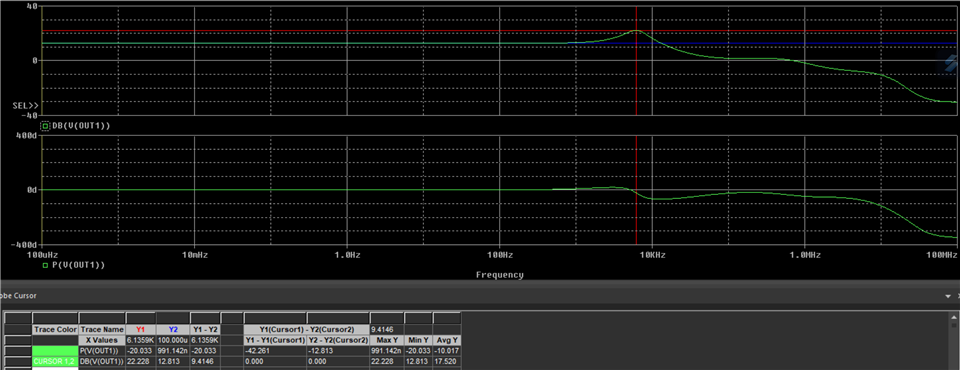
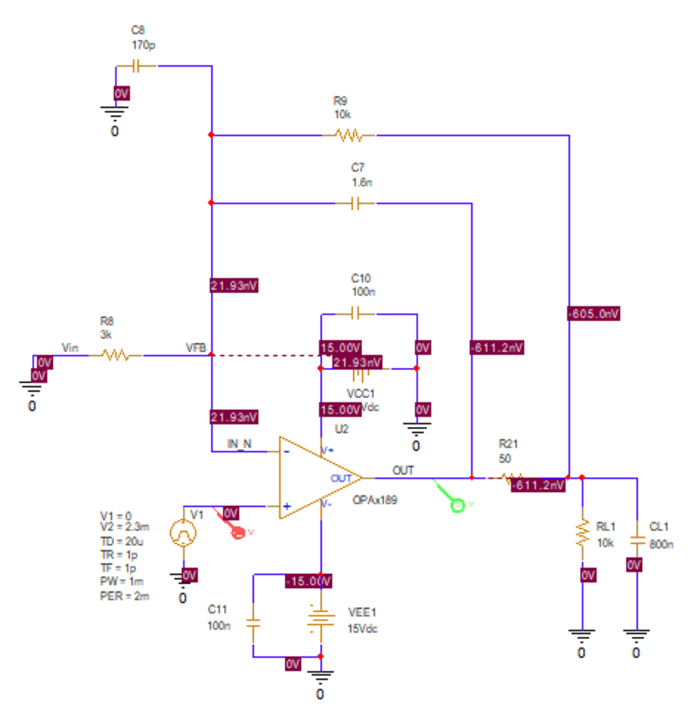
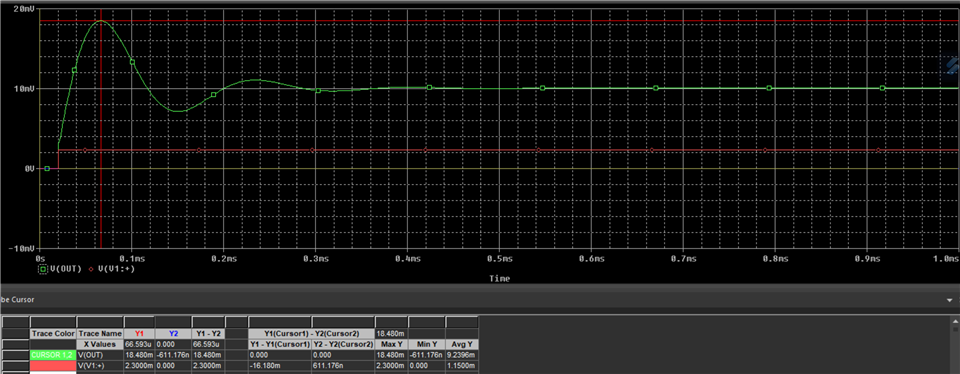
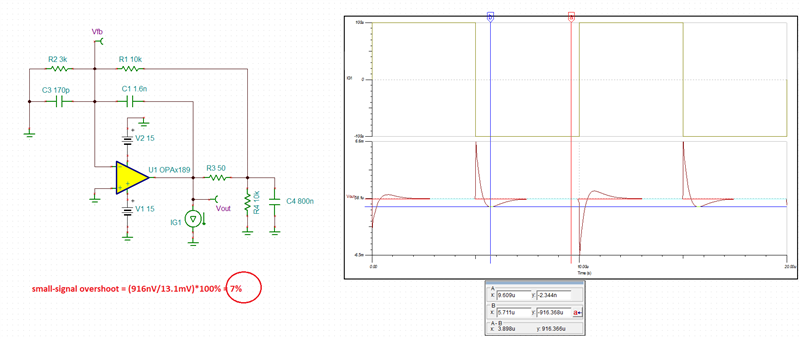
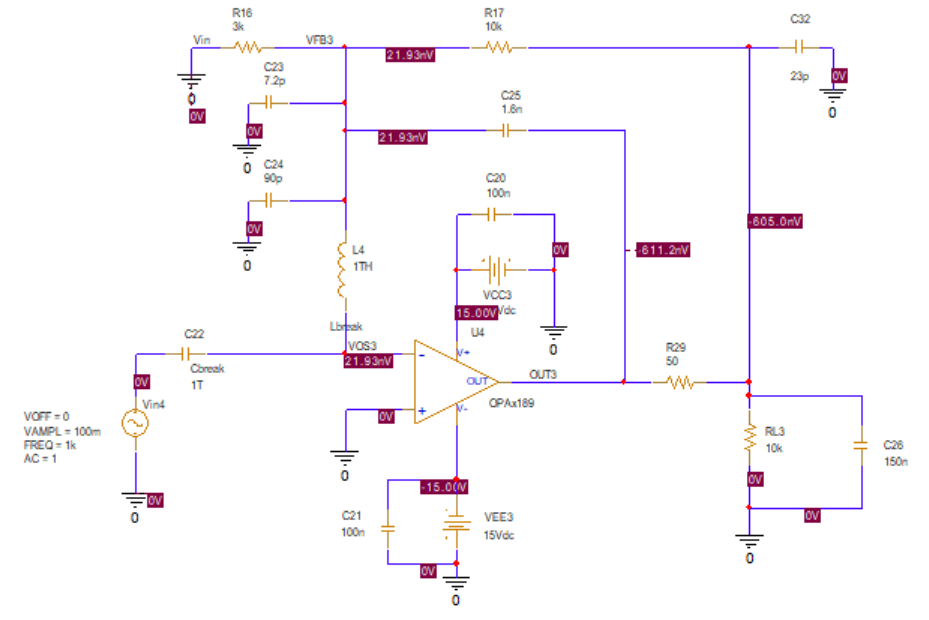
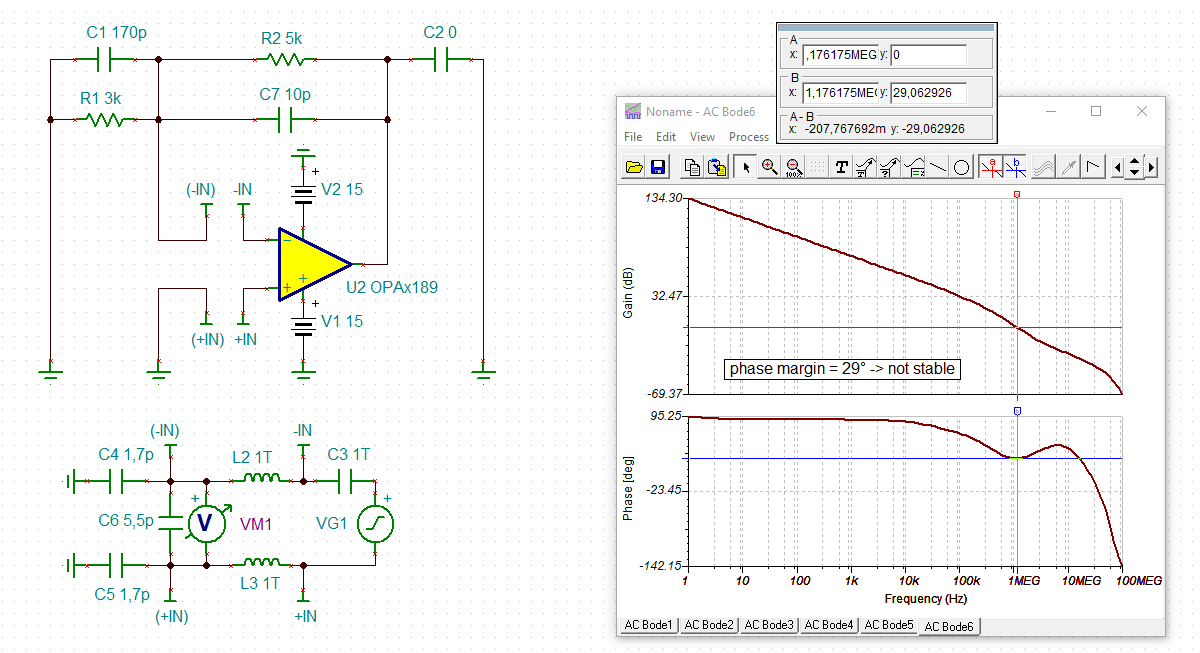
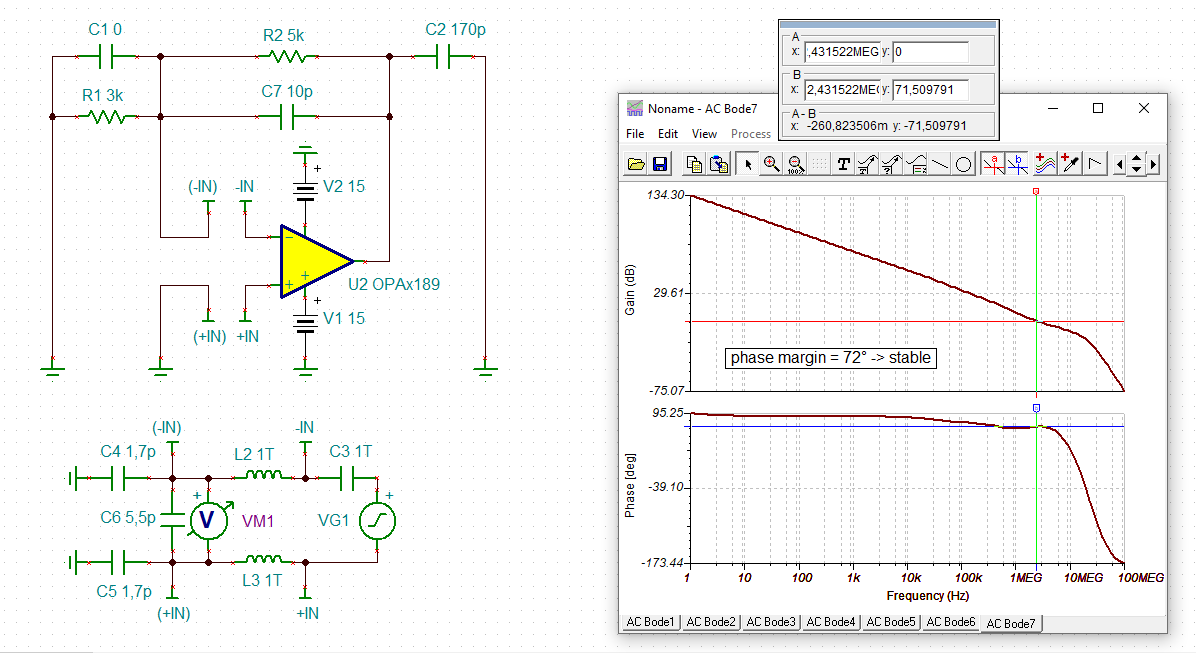
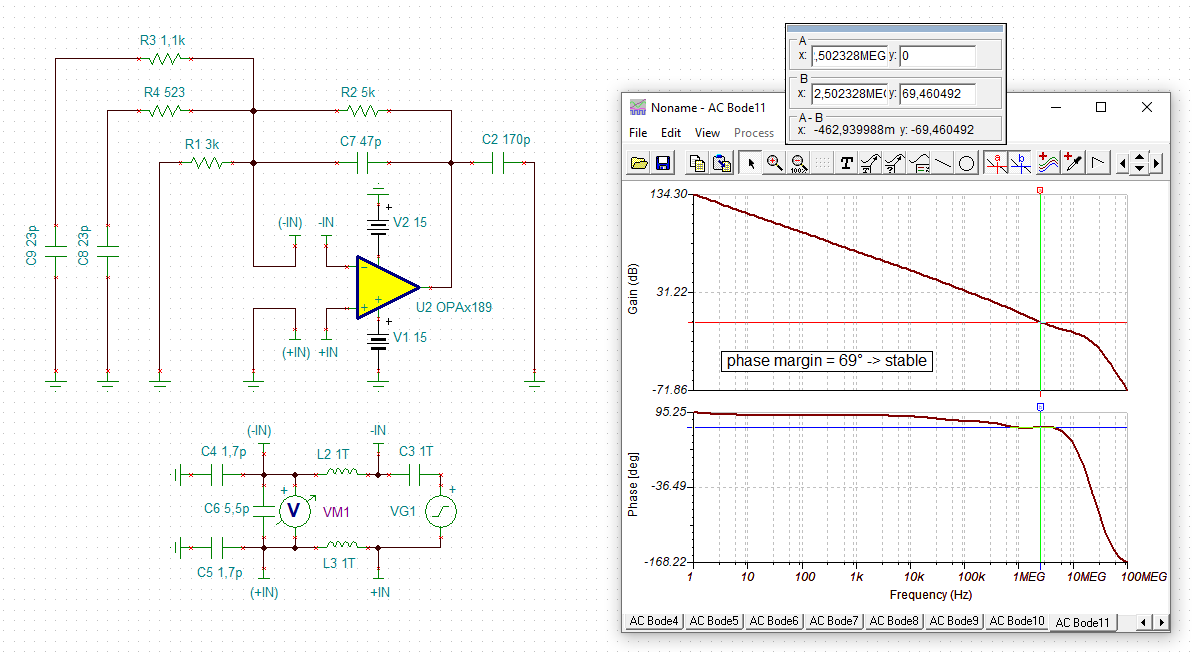
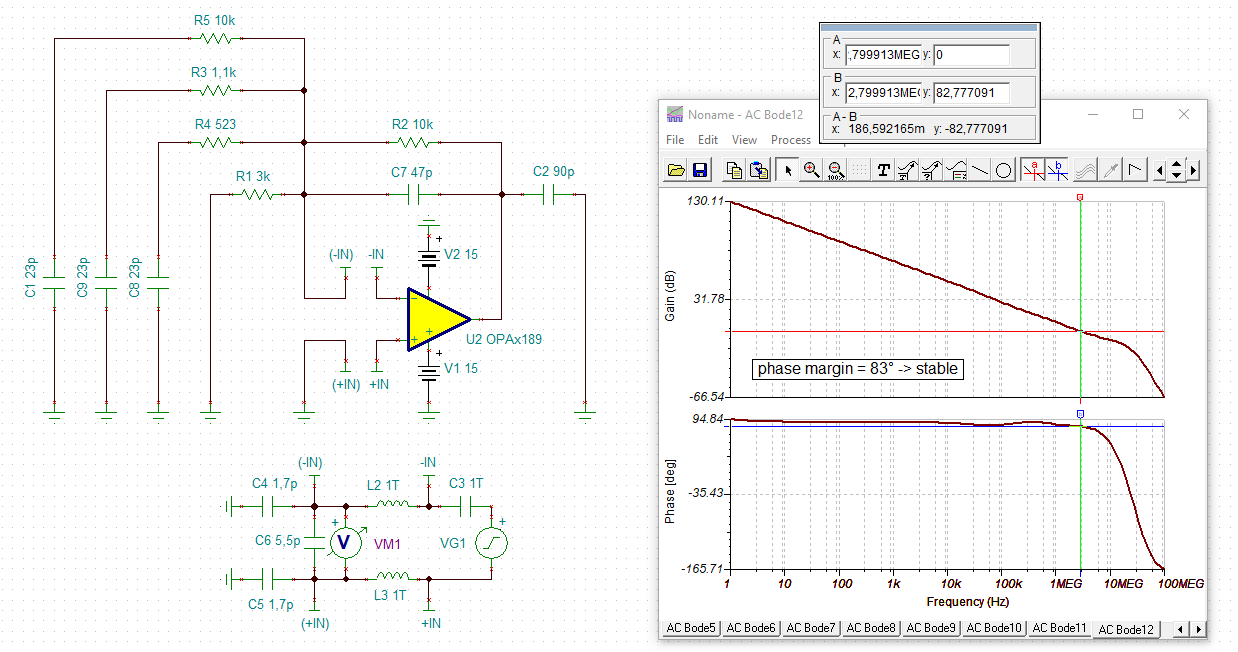
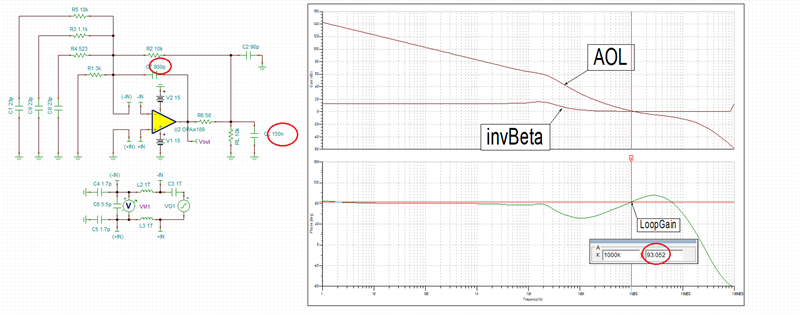
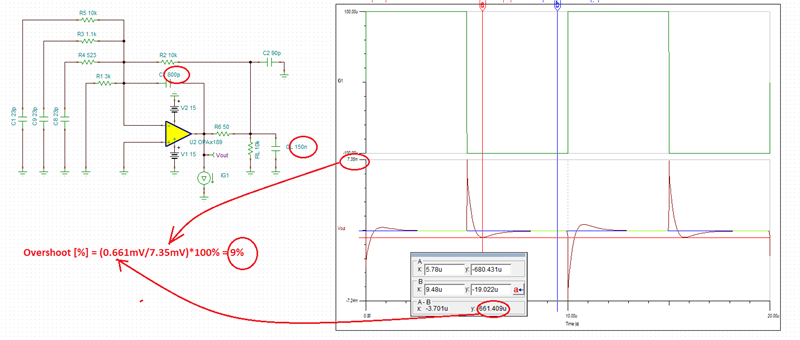
I am trying to simulate open loop gain and determine stability using PSpice for TI for the following circuit (component values are not determined yet, but circuit configuration is). I would like to make sure I am opening the loop correctly and plotting the appropriate parameters. I would like to plot Aol, 1/B and AolB phase. Any help is appreciated!