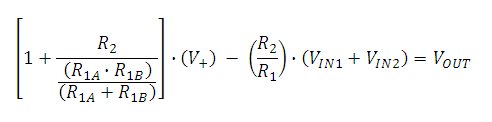I am following the advice on Application Report SLOA058 Figure 7 to use an OPA340 as a summation circuit.
I am using a Vcc of 5V, R1A = R1B = R2 = 1kOhm (for gain of 1) so R3 = 330Ohms (There is no R1C in my circuit, only two inputs).
I have set up a difference circuit (Figure 8) with no problems, however the summation circuit is giving an unexpected output.
By KCL:
(((Vin1)-(V-))/R1A)+(((Vin2)-(V-))/R1B) = (((V-)-(Vout))/R2). [Eqn 1]
For an ideal op amp (V-) = (V+) = 0, so Eqn 1 becomes
(R2/R1)(Vin1+Vin2) = Vout [Eqn 2]
for equal R1A and R1B. This gives the desired summing effect with gain (R2/R1).
However, by testing I have found that (V-) does not equal (V+) (a difference of half a volt) and neither equate to zero. So while the first equation is still found to be valid it does not become the second equation and the summation effect does not occur.
Any suggestions as to why V- does not become 0?