• State Resolved
  • Locked Locked
  • Replies 5 replies
  • Subscribers 47 subscribers
  • Views 2799 views
  • Users 0 members are here
Support feedback
Options
Options
Related

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

THS4131: Noise response with hi value resistors

Elder Costa17
Expert 2825 points
Part Number: THS4131
Other Parts Discussed in Thread: OPA2140, THS4541, TINA-TI

I am troubleshooting a circuit with the THS4131. It is a new version of an old design where the THS4131 is also used and whose performance is OK. The problem is the original designer used high value resistors, 47kOhms and 4.99kOhms (so gain ~9.4) on the feedback network. I know, these values are way higher than the prescribed by the data sheet. However, in our design the THS4131 is used for its differential feature and its low noise, not its high speed (it amplifies an amplitude modulated 125kHz sinewave), so bear with me.

The circuit before the differential amp is the same as the original design, the main change is the ADC it feeds. However, we are finding a higher noise with this new design. We are trying to locate the source of noise and, so far, the AD has been discarded (its performance meets the expectes from data sheet). We then connected the differential amp and short-circuited its inputs the the common mode node of the AD (actually, to the voltage follower of it - an OPA2140).

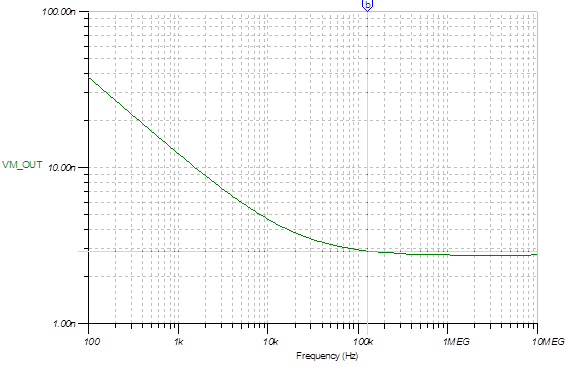
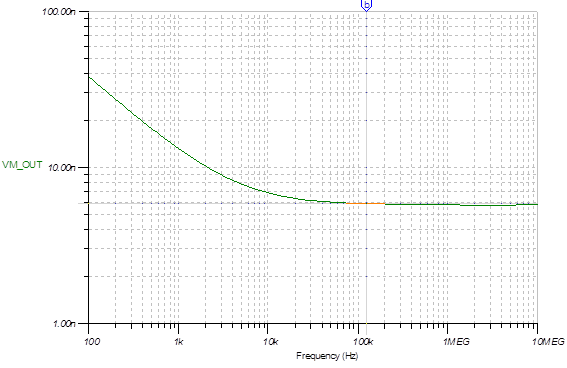
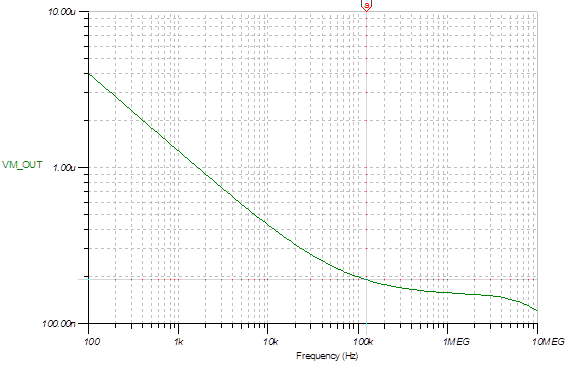
We performed a data capture with a couple thousands samples and ran an FFT and we noticed a 1/f like response that extends through around 300kHz. This noise is the reason for this post because as per the data sheet both input voltage and current equivalent noise has a knee around 1kHz and we are seeing it happen around 300kHz. What could cause this 1/f (kind of) noise? At 125kHz the noise level is much higher than on the flat noise range (some 4 to 6 times) thus demodulating it results in higher output noise, making the circuit unsuitable for the application.

FWIW I have done a noise estimation of the circuit based on an article by Michael Steffes in EDN as well as the section 8.5 of THS4541 data sheet cited there. I did not consider the 1/f noise because of the knee at 1kHz that is not relevant for my application and considered a bandwidth of 2.5kHz due to the demodulation. The resulting noise is lower than what we are observing on the FFT and, anyway, it was supposed to be flat on the range considered.

So the question is could the use of higher value resistors be the cause of this 1/f behavior? Or there could be another cause I am missing?

Also, could the THS4131 be used with higher value resistors than the 390R in the data sheet, say, Rg=1k, Rf=10k-ish? I would not like to use low values because power consumption and heat sinking are critical in this design.

FWIW the sampling rate is 5MSPS, FFT buffer size is 2000 18-bit samples.

Thank you all in advance for any hint.

  • 0
    Expert 2825 points

    I have  worked on the subject a litlle furter. I have taken the Tina-TI file from the thread below and done some tests of my own varying the resistors.

    https://e2e.ti.com/support/amplifiers/high_speed_amplifiers/f/10/t/550839?tisearch=e2e-quicksearch&keymatch=ths4131

    The first thing I noticed is even with the "ideal" resistors (i.e. temperature set to -274C), the knee is far from the 1kHz whereabouts (about 20kHz in this case).

    When I take resistors into account, I get this, still way above 1kHz:

    Finally, with the values of my circuit (i.e. 5k/47k), I get this:

    Notice the knee around 100kHz. Is this right? Is there something with the model? What am I missing?

    Again, thanks in advance for any hint on this.

  • 0 in reply to Elder Costa17
    TI__Genius 15975 points

    Hi Elder,

    If your system is sensitive to noise, then the only way I can think of in-order to reduce noise is by reducing the Rf. If you deduce the output noise equation below for a fully differential amplifier such as the THS4131, the input current noise (In) and 4kTR noise are not a major factor unless the Rf is increased significantly. With a higher value of Rf, the input current 1/f noise gets multiplied by Rf which looks like an increasing shift of 1/f corner to the right.

    So, the suggestion would be is to make Rf as 5k and Rg as 500 or lower in-order to meet your system noise requirement.

    Best Regards,

    Rohit

    where, Eni and In include both the 1/f and flat-band noise.

  • 0 in reply to Rohit Bhat
    Expert 2825 points

    Hello Rohit,

    First of all, thank you very much for your answer.

    Yes, I agree the lower the resistors the better. It turns out since I last posted I was able to evaluate the impact of the differential amplifier over the system noise and I found it is not the culprit for the noise we are observing, even with the higher resistor values. I intend reducing the values anyway to improve noise margins and system performance.

    The question that is still open is why the knee on the noise density moves rightward as resistor values increase? Also why does the simulation not match the data sheet even with the nominal 390 Ohms resistors for Rg and Rf? Model limitations or there are other factors I am missing?

    I notice in the first figure of your message and equation for eno, the Rg noise is missing. Is that right? I have made a spreadsheet and the contribution of Rg noise is significant in most cases, with the noise caused by In second. Rf noise becomes relevant when gain is 1.

    Again, thank you very much for your support.

    Best Regards.

    Elder.

  • 0 in reply to Elder Costa17
    TI__Genius 15975 points

    Hi Elder,

    I think the primary reason for the 1/f corner of output noise to shift towards the right is due to the increase in feedback resistor (Rf) value. The input current 1/f noise is multiplied by the Rf which changes in a log fashion from 47k to 390 ohms and thus, seems like an increasing shift of 1/f corner to the right.

    This is better understood by calculating the individual noise contributions that make up the THS4131 output noise, which I have copied from above. If we keep the noise gain (1+Rf/Rg) constant for different values of Rf, the noise contribution at the output due to the input voltage noise (eni) stays the same regardless of the Rf you choose. However, this is not the case for the current noise contribution at the output because the current noise is multiplied by the absolute value of the Rf. As a result, a logarithmic change in Rf from 47k to 390 ohms will cause this 1/f corner shift because the current 1/f noise (In_1/f) itself has a logarithmic shape to it.

    If you look at the graph above for TINA-TI simulation of output noise across various Rf and Rg, you will notice that the noise gain (1+ Rf / Rg) ~ 11 stays constant independent of Rf. This means the input voltage noise contribution at the output stays the same regardless of Rf. However, the Rf absolute value is changing as well, which will shift the output noise 1/f corner frequency due to its multiplication by the current noise 1/f (In_1/f).

    Output noise expression for a fully differential amplifier (FDA):

    where, Eni (input voltage noise)= Eni_1/f + Eni_spot and In (input current noise) = In_1/f + In_spot

    Graphical representation of 1/f shift due to Rf:

    I believe the TINA-TI simulation does match the datasheet with the nominal 390 ohms resistors for Rg and Rf. I think you should compare the input referred noise (not the output) in the TINA-TI simulation with the noise mentioned in the datasheet.

    The Rg noise is part of the Noise gain expression for the output voltage noise (Eno). I would recommend you to go through the App-note of noise analysis for fully differential amplifier to better understand the problem:

    Best Regards,

    Rohit

  • 0 in reply to Rohit Bhat
    Expert 2825 points
    Hello Rohit, that clears things up.

    Thank you very much.

    Elder.