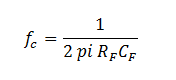Hello Team,
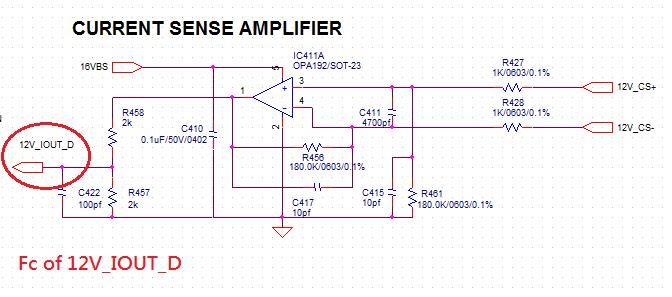
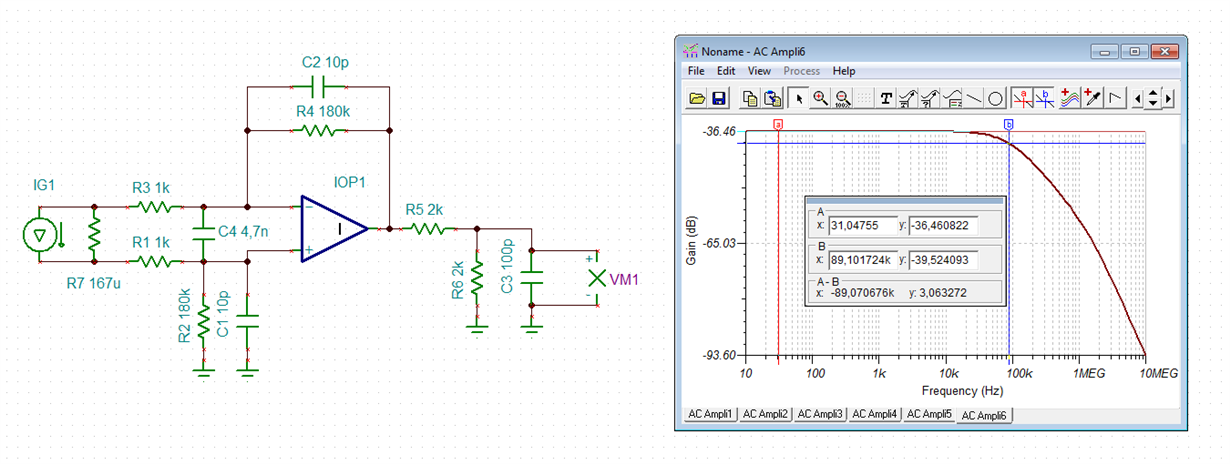
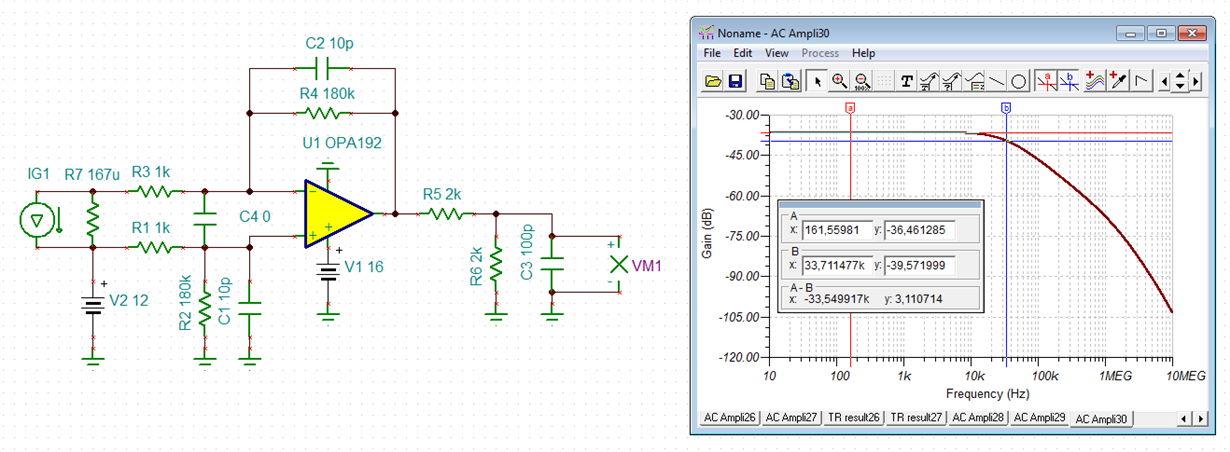
My customer is using OPA192 as current sense amplifier, the CS resistor is 0.167mohm, based on the schematic they have, how's the the cross over frequency looks like? and how to calculate? because the CS resistor is too small, it's hard to do real test, can you tell how to calculate the fco?
Thanks.
Martin
Hi Martin,
low pass corner frequency is about 90kHz:
Take care, C411 can make the OPA192 unstable! I would remove it.
Kai
Hi Martin,
in the following you will see the frequency response and the transient response of your circuit:
It was current signal through the shunt simulated of 15ADC, superimposed by a 1kHz square wave of 10A amplitude. The corner frequency of low pass filtering is about 40kHz. The frequency response shows a resonance and the transient response shows a heavy ringing.
Omitting C4=4n7 yields the following simulations:
Corner frequency of low pass filtering is arround 34kHz now and the transient response is almost free of ringing.
Kai
Hi Martin,
The low-pass cutoff frequency is about 90 kHz, as Kai indicated. You can see the filter response in the TINA screenshot seen below. The circuit transfer function is provided within that screenshot.
Regards, Thomas
Precision Amplifiers Applications Engineering
Hi Martin,
The reason that Kai's second simulation has a lower cutoff frequency is due to the roll-off of the OPA192 open-loop gain (Aol) coming into play in the gain vs frequency response of the circuit. The ideal op amp doesn't exhibit the pole that introduces this effect. It was used purely to obtain the ideal transfer function. The OPA192 response adds the second pole to the overall response and simulation shows that the roll-off has increased to that of a second-order roll-off (40 dB/dec), vs the first-order roll-off (20 dB/dec) obtained with the ideal op amp.
If the input filter configuation is modified such that the 4.7 nF is moved from across the OPA172 inputs, to one each 4.7 nF from each input to ground, the inverting input will still have a large capacitance connected to ground. Likely, there will still be stability issues. Also, the filer changes from a differential filter to a combination differential/common-mode which may or may not help with the noise issue.
There is a way to design an input filter that moves the large capacitance away from the op amp inputs. That is to split each input resistor into two, and connect the capacitor where each set of the resistors meet. I show an example of this below; however, it does change the transfer function and that needs to accounted for when designing the circuit.
Note that in this ideal op amp case there are poles associated with the input network, and the networks in the feedback loop and at the non-inverting input. This results in a second-order roll-off (40 dB/dec). The components would have to be determined to satisfy the specific cutoff and roll-off requirements of the overall circuit.
Regards, Thomas
Precision Amplifiers Applications Engineering
Hi Martin,
If the PC board cannot be changed to accommodate the split input resistors and capacitor, then you have to work with the existing component spaces. One possible option is to remove the 4.7 nF capacitor across the OPA192 inputs, and use the feedback capacitor (C417) and the one from the non-inverting to ground (C415) to set up the low-pass -3 dB cutoff frequency. This only results in a first-order low-pass (-20 dB/dec), but if the cutoff frequency can be set low enough to reduce higher frequency noise the performance may be acceptable.
I show below an example of the OPA192 set up for a cutoff frequency of 1 kHz. The cutoff is determined by:
The C415 capacitor is set to the same value as C417. For this example the capacitors are 884 pF.
I have attached my OPA192 TINA file for your use.
Regards, Thomas
Precision Amplifiers Applications Engineering
