Hi
I am going through TI precision labs (Opamps) -- Stability series. I have a question about the calculation method suggested for R_iso
Video could be found at
https://training.ti.com/ti-precision-labs-op-amps-stability-5?cu=14685
The pdf of this video course is:
https://training.ti.com/system/files/docs/1335%20-%20Stability%205%20-%20slides.pdf
& the exercise is at:
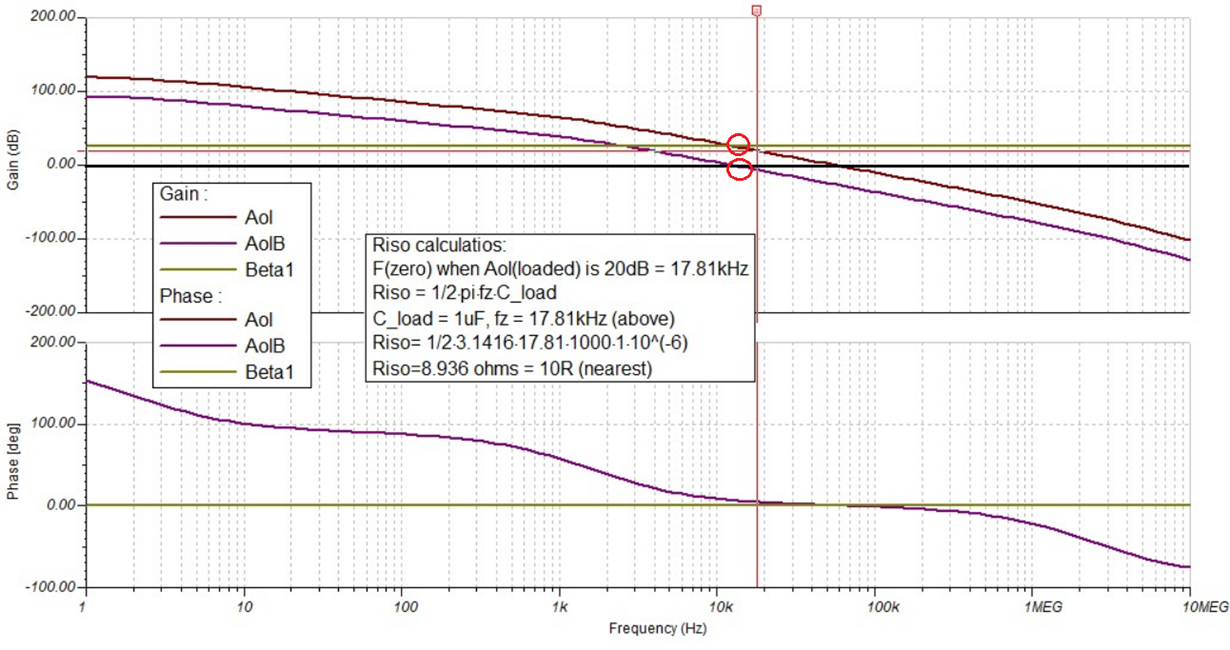
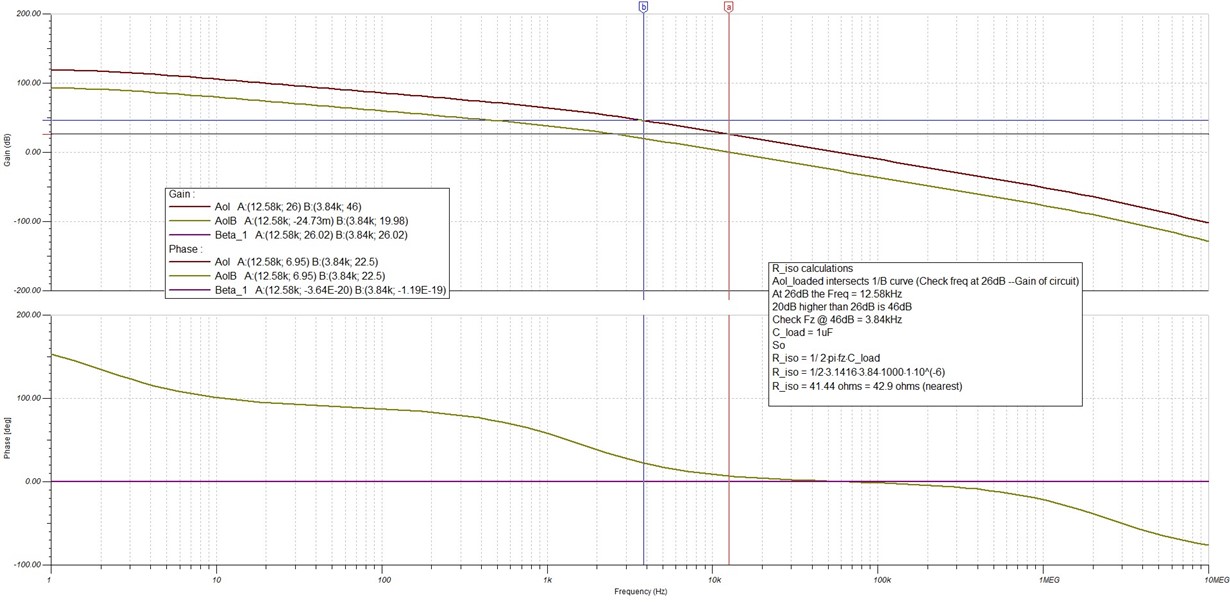
In this video (on page 13) of the above link (pdf to video course material),it states the Design Steps to calculate the value of Riso
1) Find the zero frequency , f(zero) when AOL_LOADED = 20dB
Now, the equation of AOL_Loaded is given on page-3 of same pdf as:
AOL_Loaded = Vo/Vfb
But when I look at the solution of Exercise (problem-2)
It seems like it is getting a value of 3.7kHz (@20dB). When I simulate the same circuit, I get fz = 17.81kHz @ 20dB for Aol_Loaded plot). However, I get 3.83kHz @ 20dB for AolB (loop gain plot)
(See my plot picture below):
So, my question is: which plot do we use to calculate the Riso value? Aol_loaded or AolB?