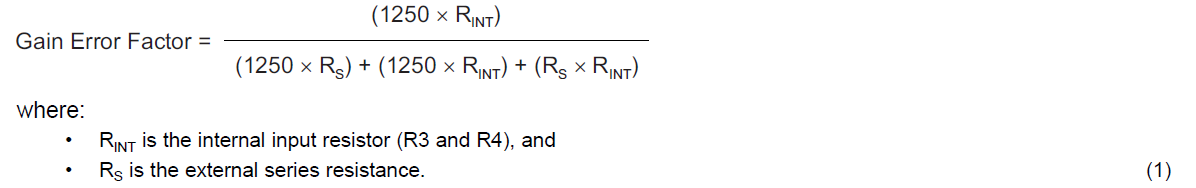Other Parts Discussed in Thread: INA186
Hi support team.
I received some inquiries from my customer.
Customers had to protect the device from destruction with a complete system, and they had to increase the input resistance inevitably.
Is the calculation result when RINT is 1.3k-2kohm in the following formula usable?
If No, what will happen?
Currently the value of Rint is less than 10ohm.
I appreciate if you provide some information regarding it.
Let me know if you have any question.
Thank you for your cooperation.
Best regards,
Higa