Hi there,
We have selected ADS124S06 for Bridge sensor.
Bridge sensor specifications:
1. Excitation voltage : 3.3V
2. Sensitivity : 2mV/V
3. Capacity : 2Kg
Our required Programmable data rate is 2000kSPS.
By setting this, We are getting Peak-to-Peak noise as 2.8uV (By using Analog Engineer's calculator).
Using these data, We are getting only 14.168 Bits(Noise free bits) - 2357 Counts instead of 24 bits. By using this formula,
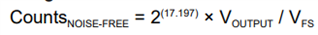
Refer : ADS1x4S08 Evaluation Module User's Guide (Rev. A)
How to get maximum Effective number of bits (ENOB)? How to reduce noise for High sampling rates?
Kindly give your suggestions on this.
Thanks & Regards,
Sneha K