Have you ever wondered how delta-sigma analog-to-digital converters (ADCs) can get such fine resolution across a variety of bandwidths? The secret lies in the digital filter. Delta-sigma ADCs are different from other types of data converters in that they typically integrate digital filters. In this first installment of a three-part series, I will discuss the purpose of the digital filter as well as a few types of digital filters commonly used with delta-sigma ADCs.
To understand why the digital filter is an important aspect in delta-sigma analog-to-digital conversion, it is critical to have a basic understanding of a delta-sigma modulator. Joseph Wu wrote a very helpful Precision Hub post that explains the transformation of analog input signals into a digital bitstream.
When you plot the spectrum of quantization noise in a delta-sigma modulator, you’ll see that quantization noise is denser at higher frequencies. This is the infamous noise-shaping that delta-sigma ADCs are known for. In order to reduce quantization noise, you feed the modulator output to a low-pass filter.
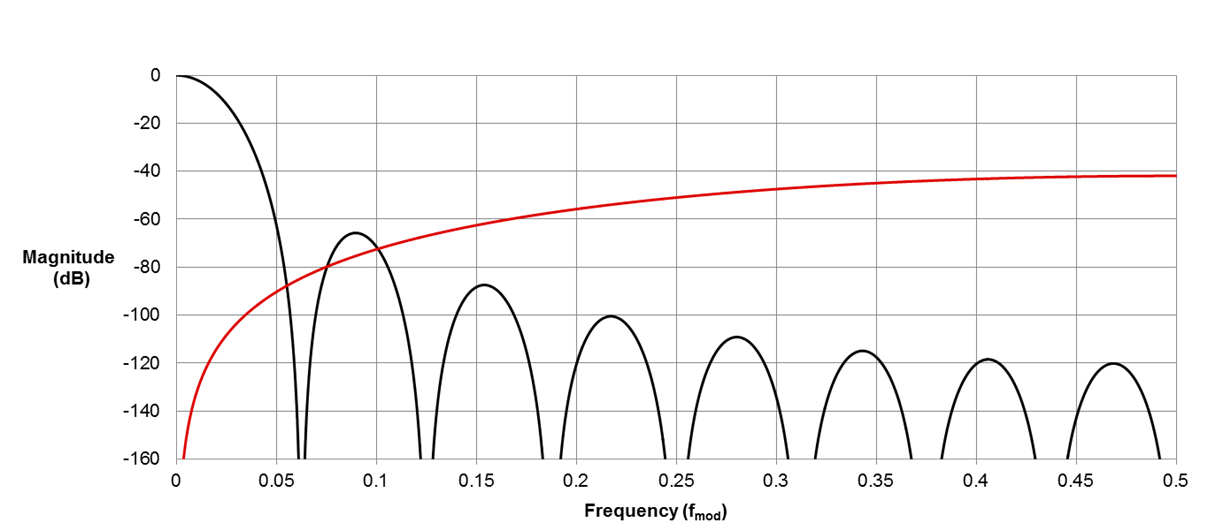
Figure 1 shows quantization noise plotted with the response of a common type of low-pass digital filter found in delta-sigma ADCs called a sinc filter (its name stems from its sin(x)/x frequency response).
Figure 1: Spectrum of delta-sigma quantization noise and a sinc low-pass filter
Sinc filters, while extremely common, are not the only types of digital low-pass filters associated with delta-sigma ADCs. For example, some ADCs, like the ADS1220, add an extra 50Hz/60Hz notch filter designed for applications with a lot of power-line interference. One the other hand, the ADS127L01 has a wide-bandwidth flat-passband digital filter designed for higher-frequency applications.
As my colleague Ryan Andrews explained in his post about anti-aliasing filters, the digital filters in delta-sigma ADCs serve another function – decimation. These filters decimate the modulator sampling frequency and output data at a much lower rate (fDR) by a factor known as the oversampling ratio (OSR). The OSR and filter type combined determine the digital filter’s output bandwidth. Large OSRs produce small filter bandwidths, which translates to very good noise performance, simplified anti-aliasing front ends and reduced interface speeds for the host controllers.
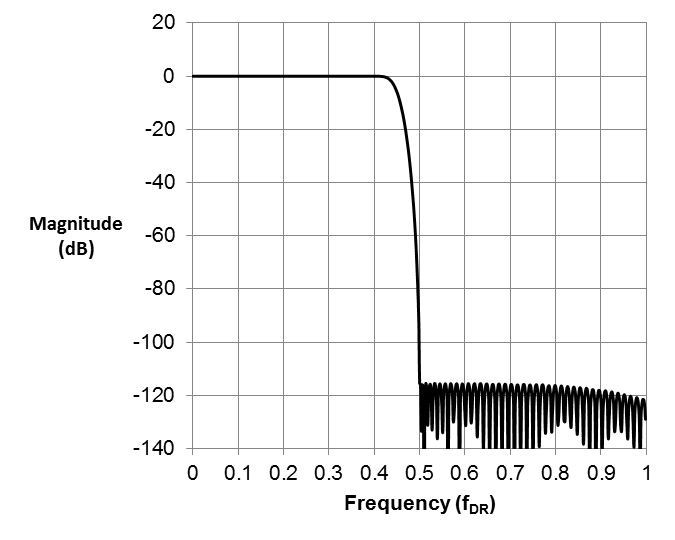
Most digital filters have a finite impulse response (FIR). These filters are inherently stable and easy to design with linear phase responses. Let’s compare two types of FIR filters in delta-sigma ADCs. The first is a wideband filter in the ADS127L01. The second is a classic third-order sinc response filter, or sinc3. Figures 2 and 3 plot these responses side by side.
 |
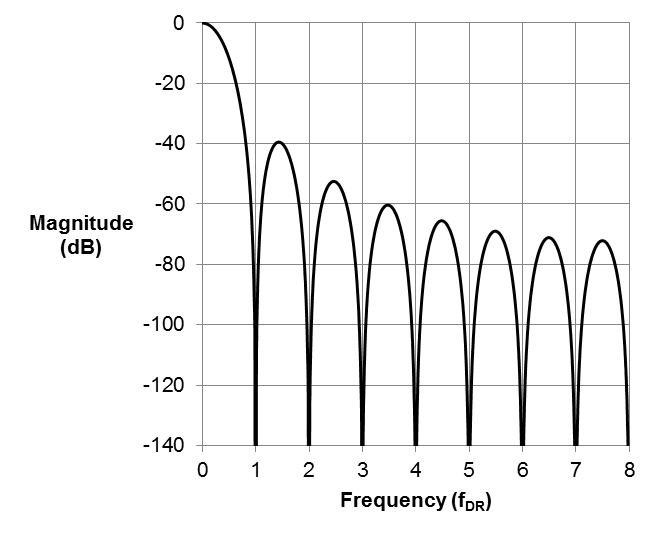 |
| Figure 2: Wideband filter frequency response | Figure 3: Sinc3 frequency response |
Right away, you can clearly see the benefit of using a wideband filter for alternating current (AC) measurement applications. Its nearly 0dB gain until right before the Nyquist bandwidth of the data rate (fDR/2) ensures no signal power loss for frequencies in the passband. The steep transition band limits aliasing. The sinc3 filter, on the other hand, attenuates signals to -3dB by 0.262 x fDR and transitions slowly even after fDR/2, which would enable more out-of-band noise to fold into the bandwidth of interest. Seemingly, the wideband FIR filter would be ideal for any application; however, this excellent frequency-domain performance comes at a price.
The trade-off between the wideband filter and the sinc filter is in the time domain. The wideband filter is a very high-order filter, which means that it takes a long time to settle to a final value upon receiving a step input. In the ADS127L01’s wideband filter, you will have to wait 84 conversions to receive a settled output. A sinc3 filter settles in three conversions after a step at the input, enabling you to cycle through multiple sensors. This trade-off between frequency response and latency exists for all FIR filters.
In my next post (coming in a few weeks), I’ll peek behind the curtain of sinc filters, including what determines the settling time in sinc filters and how you can modify some of them to reject additional frequencies of interest. In the meantime, subscribe to Precision Hub to receive notifications when my next two posts are live.
Additional resources
- Find more than 100 data-converter technical resources in our Data Converter Learning Center.
- Download the e-book, “Best of Baker’s Best: Delta-Sigma ADCs” (myTI login required).
- Check out the TI E2E™ Precision Data Converter forum for more sinc filter insight.
- Explore TI’s portfolio of precision ADCs and find related technical resources for your design.