Other Parts Discussed in Thread: OPA3S328, TINA-TI, ADS1675, LMP7721, LMP7715
Hello Experts,
Our customer has a technical question about the product OPA3S328EVM.
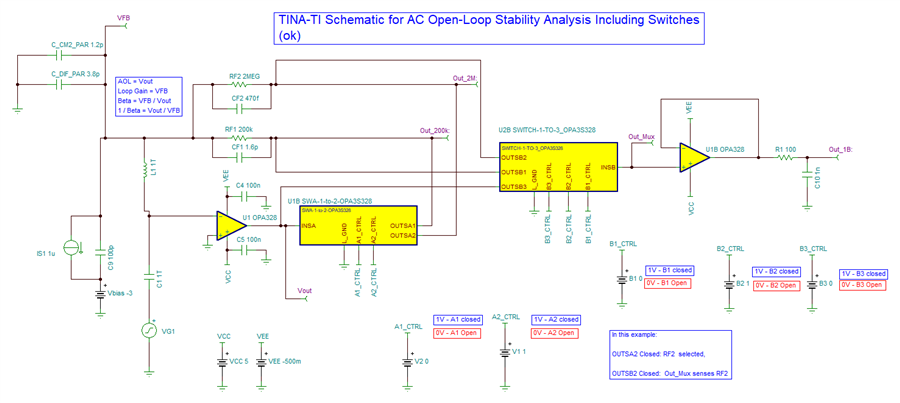
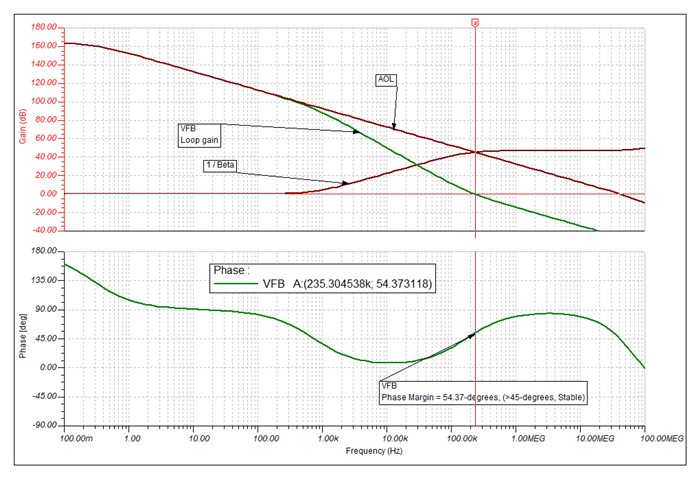
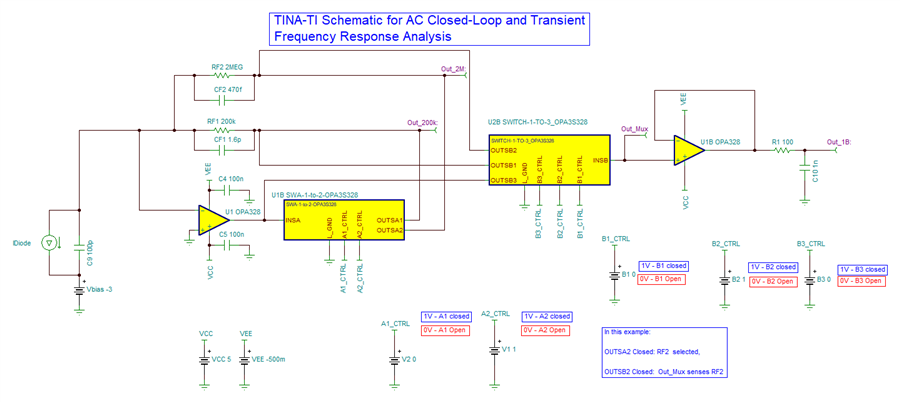
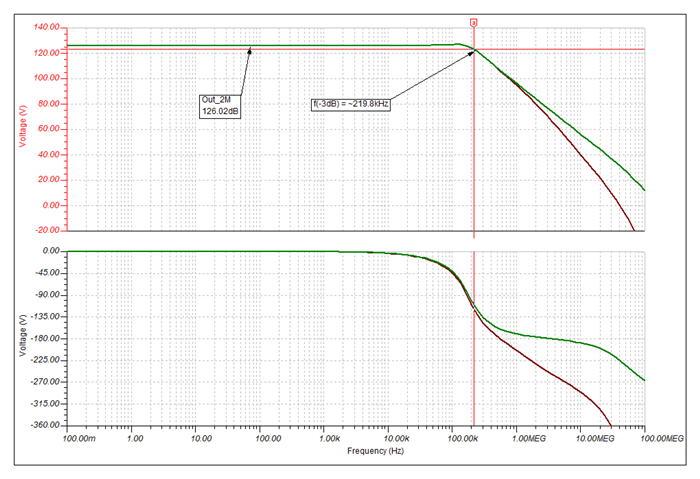
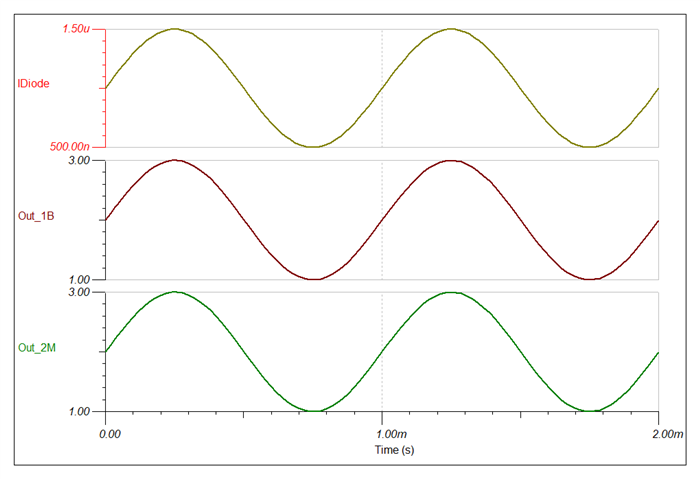
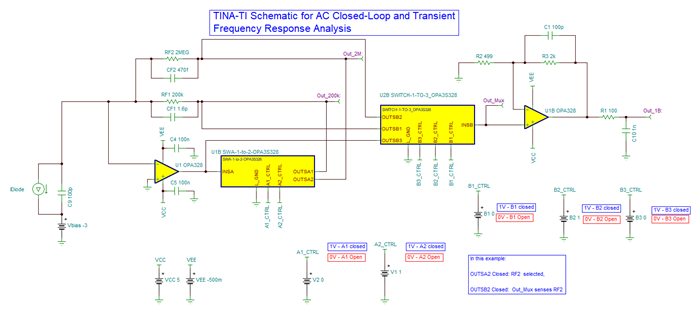
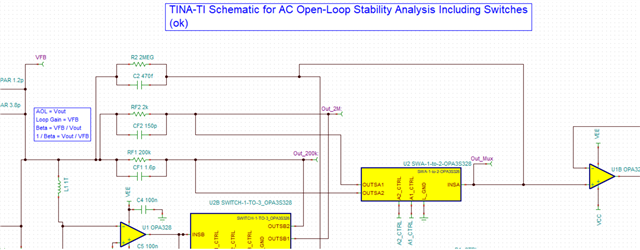
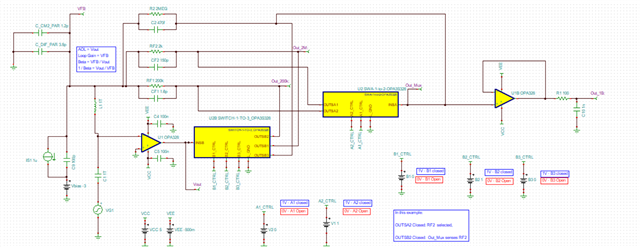
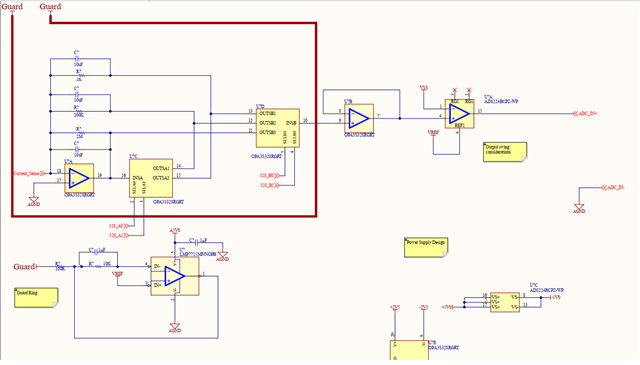
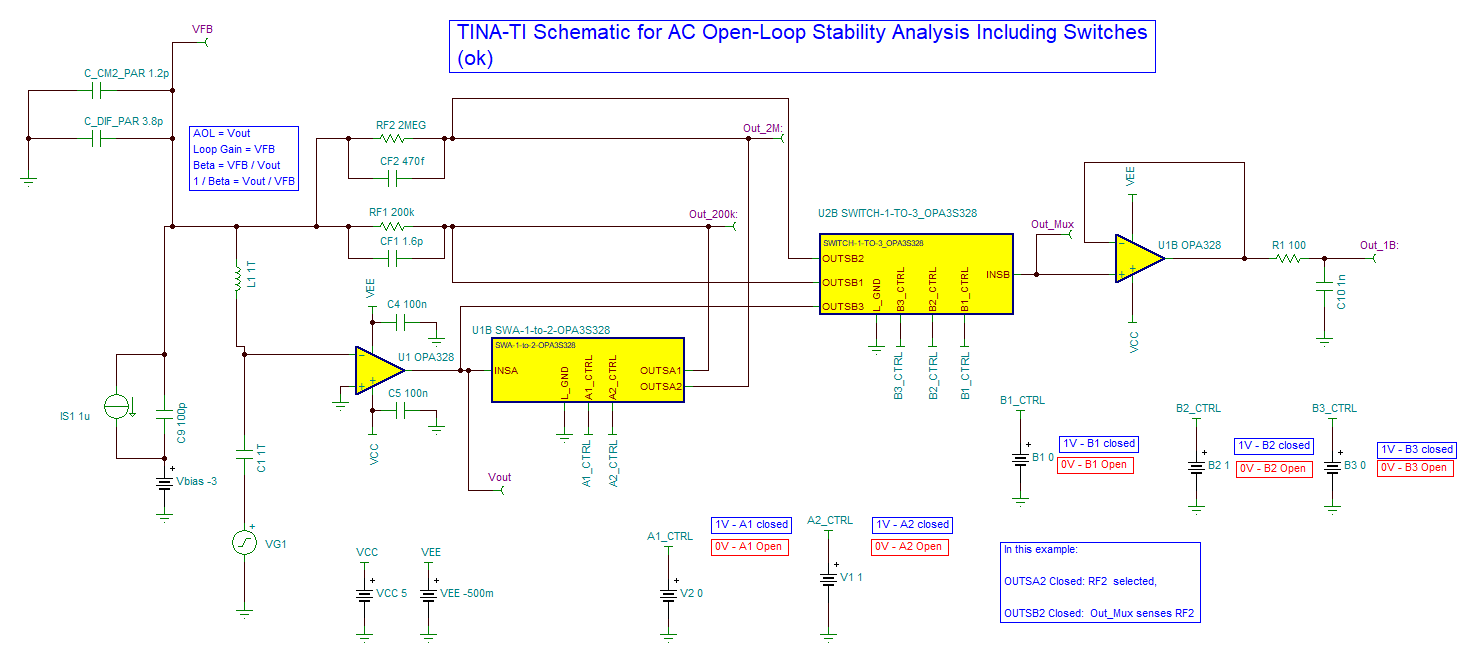
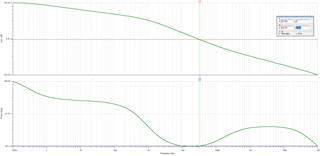
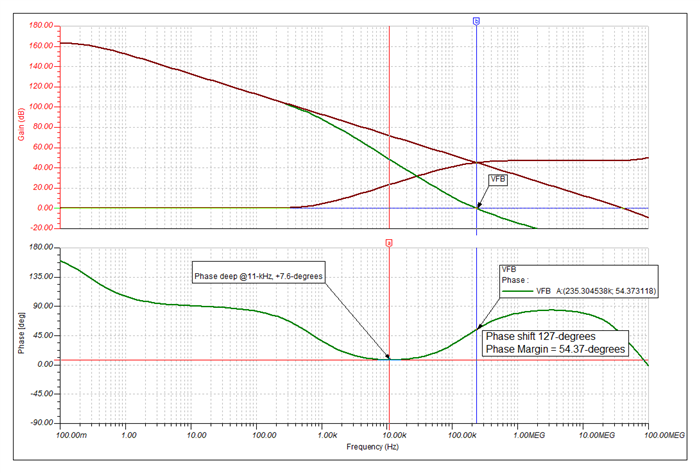
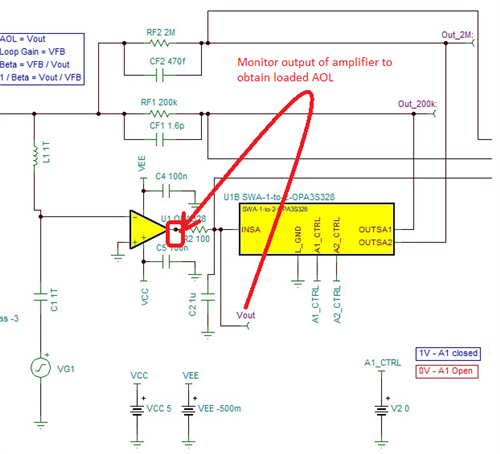
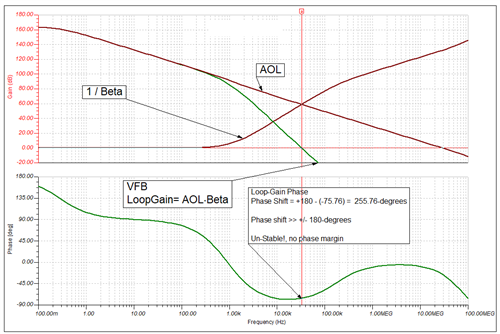
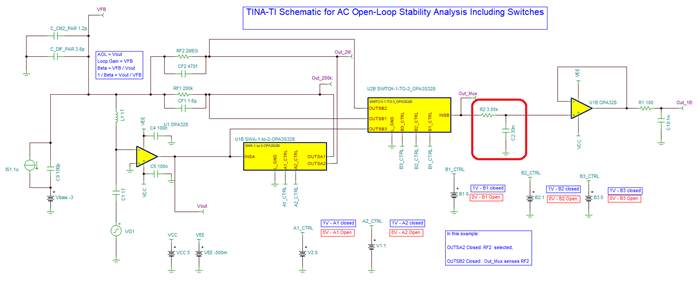
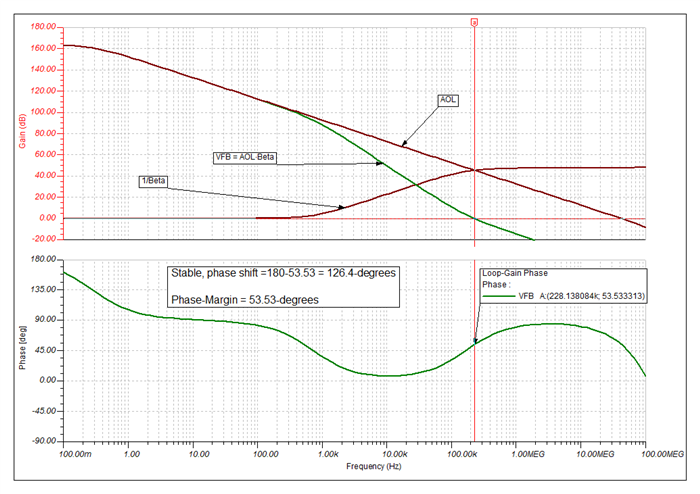
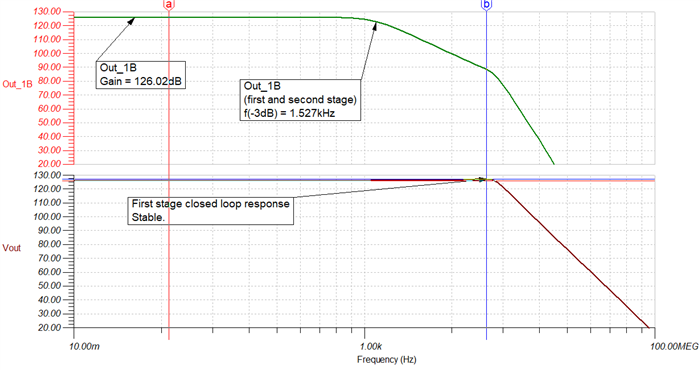
He has been going through the "Application Report: Build a Programmable Gain Transimpedance Amplifier Using the OPA3S328" and he is curious if we have tested the TIA with larger feedback resistors (~10s of Mega Ohms). The report only talks of feedback /gain of 200kV/I but not any larger.
In addition, can the customer get a spice netlist for the evaluation board? The customer already has the spice model for the TIA, obtained it from TI website. I mean the OPA3S328EVM
I hope you can help us. Thank you.
Best regards,
Gerald