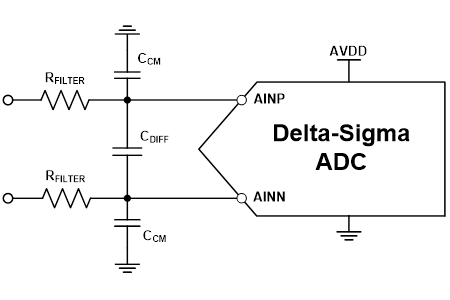
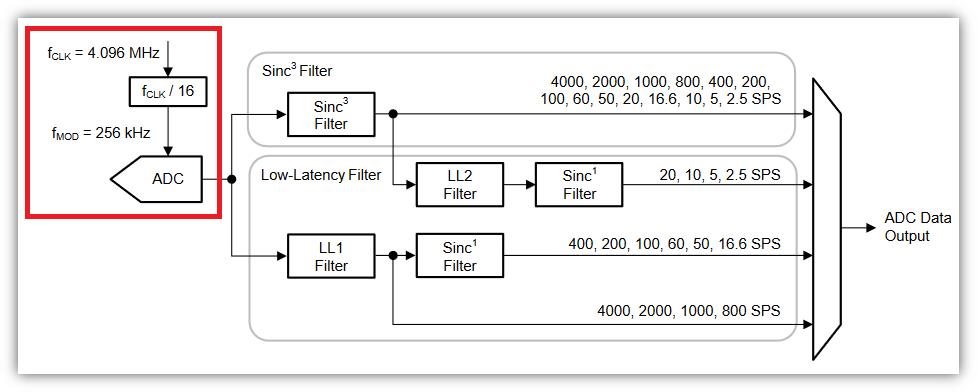
I am trying to develop a system using a low speed delta-sigma ADC for DC-type measurements. How do I select the component values for the anti-aliasing filter?
-
Ask a related question
What is a related question?A related question is a question created from another question. When the related question is created, it will be automatically linked to the original question.