Part Number: TMS320F28379D
Other Parts Discussed in Thread: C2000WARE
Hello.
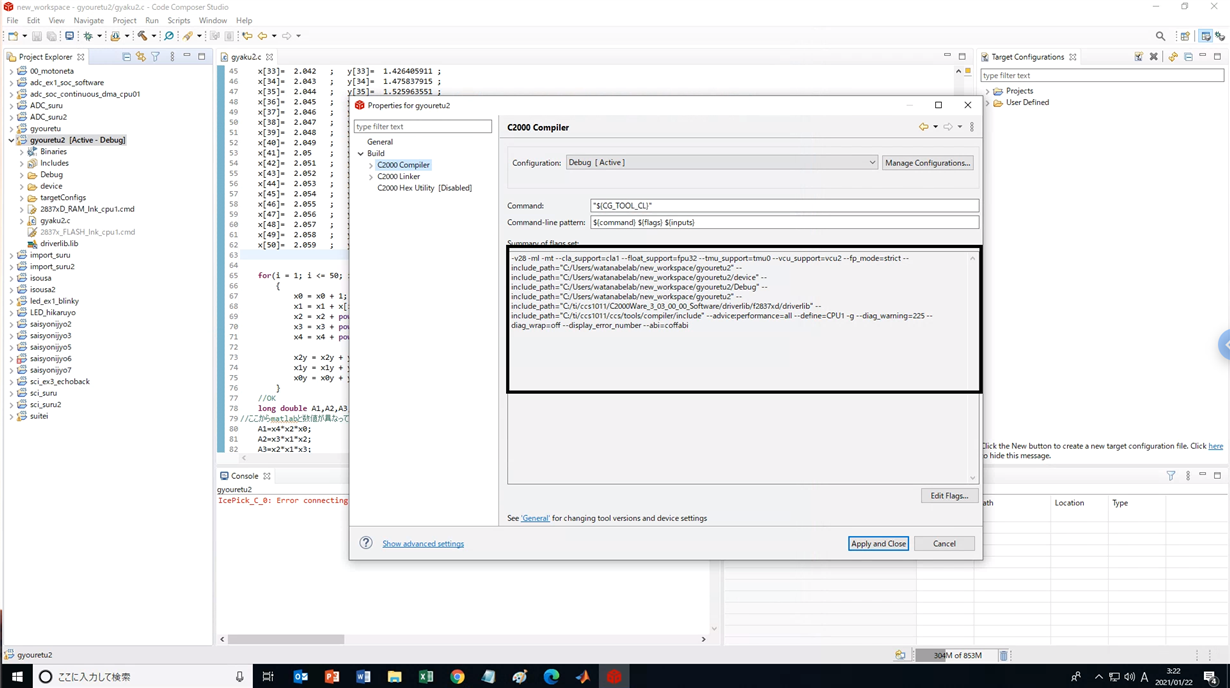
I have run the following program using CCS10.
My goal is to find the coefficients of the least squares method (quadratic function).
However, when I do the same calculation in MATLAB, I get the answer, but I can't seem to calculate it in DSP.
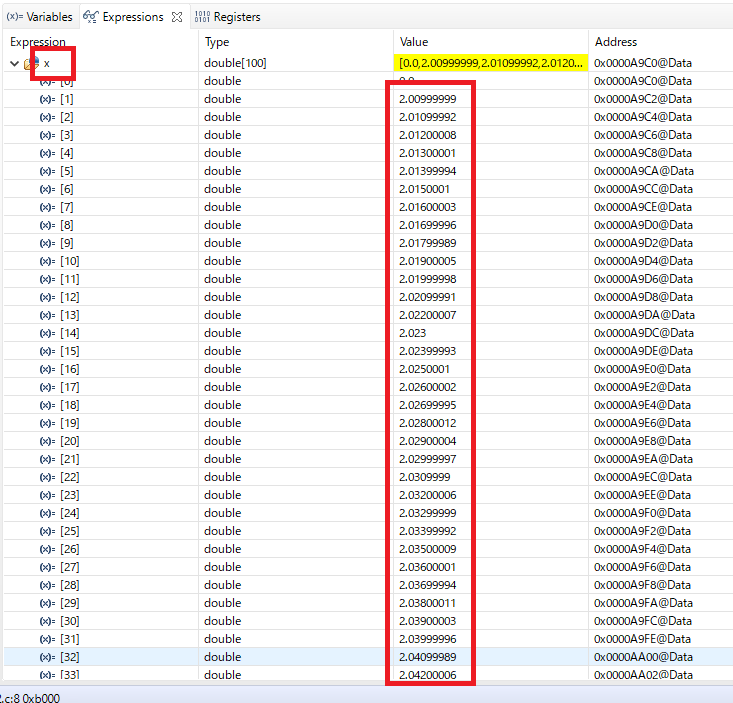
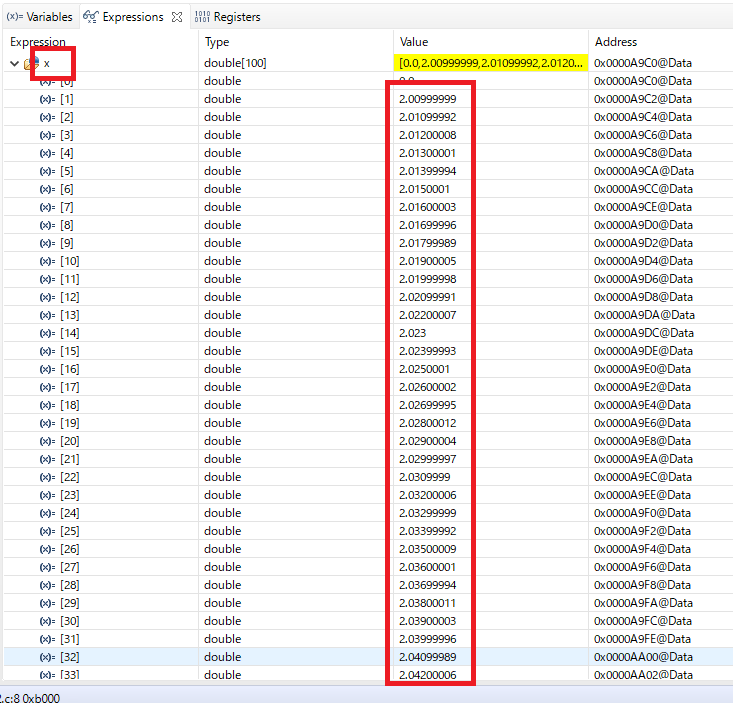
When I checked the values, there was a gap in the values from the beginning.
Is it possible to eliminate this kind of discrepancy?
Please advise.
Thanks.
#include "driverlib.h"
#include "device.h"
#include "math.h"
double x[100],y[100];
void main(void)
{
int i=0;
double x0=0,x1=0,x2=0,x3=0,x4=0,x2y=0,x1y=0,x0y=0;
x[1]= 2.01 ; y[1]= 0.211 ;
x[2]= 2.011 ; y[2]= 0.238 ;
x[3]= 2.012 ; y[3]= 0.266 ;
x[4]= 2.013 ; y[4]= 0.295 ;
x[5]= 2.014 ; y[5]= 0.324 ;
x[6]= 2.015 ; y[6]= 0.354 ;
x[7]= 2.016 ; y[7]= 0.385 ;
x[8]= 2.017 ; y[8]= 0.416 ;
x[9]= 2.018 ; y[9]= 0.448 ;
x[10]= 2.019 ; y[10]= 0.481 ;
x[11]= 2.02 ; y[11]= 0.514 ;
x[12]= 2.021 ; y[12]= 0.549 ;
x[13]= 2.022 ; y[13]= 0.583 ;
x[14]= 2.023 ; y[14]= 0.619 ;
x[15]= 2.024 ; y[15]= 0.655 ;
x[16]= 2.025 ; y[16]= 0.692 ;
x[17]= 2.026 ; y[17]= 0.730 ;
x[18]= 2.027 ; y[18]= 0.768 ;
x[19]= 2.028 ; y[19]= 0.807 ;
x[20]= 2.029 ; y[20]= 0.847 ;
x[21]= 2.03 ; y[21]= 0.887 ;
x[22]= 2.031 ; y[22]= 0.928 ;
x[23]= 2.032 ; y[23]= 0.970 ;
x[24]= 2.033 ; y[24]= 1.013 ;
x[25]= 2.034 ; y[25]= 1.056 ;
x[26]= 2.035 ; y[26]= 1.100 ;
x[27]= 2.036 ; y[27]= 1.144 ;
x[28]= 2.037 ; y[28]= 1.190 ;
x[29]= 2.038 ; y[29]= 1.236 ;
x[30]= 2.039 ; y[30]= 1.282 ;
x[31]= 2.04 ; y[31]= 1.330 ;
x[32]= 2.041 ; y[32]= 1.378 ;
x[33]= 2.042 ; y[33]= 1.426 ;
x[34]= 2.043 ; y[34]= 1.476 ;
x[35]= 2.044 ; y[35]= 1.526 ;
x[36]= 2.045 ; y[36]= 1.577 ;
x[37]= 2.046 ; y[37]= 1.628 ;
x[38]= 2.047 ; y[38]= 1.681 ;
x[39]= 2.048 ; y[39]= 1.733 ;
x[40]= 2.049 ; y[40]= 1.787 ;
x[41]= 2.05 ; y[41]= 1.841 ;
x[42]= 2.051 ; y[42]= 1.896 ;
x[43]= 2.052 ; y[43]= 1.952 ;
x[44]= 2.053 ; y[44]= 2.008 ;
x[45]= 2.054 ; y[45]= 2.065 ;
x[46]= 2.055 ; y[46]= 2.123 ;
x[47]= 2.056 ; y[47]= 2.182 ;
x[48]= 2.057 ; y[48]= 2.241 ;
x[49]= 2.058 ; y[49]= 2.301 ;
x[50]= 2.059 ; y[50]= 2.361 ;
for(i = 1; i <= 50; i++)
{
x0 = x0 + 1;
x1 = x1 + x[i];
x2 = x2 + pow(x[i], 2);
x3 = x3 + pow(x[i], 3);
x4 = x4 + pow(x[i], 4);
x2y = x2y + y[i]*pow(x[i], 2);
x1y = x1y + y[i]*x[i];
x0y = x0y + y[i];
}
//OK
double A1,A2,A3,B1,B2,B3,A;
A1=x4*x2*x0;
A2=x3*x1*x2;
A3=x2*x1*x3;
B1=x2*x2*x2;
B2=x3*x3*x0;
B3=x4*x1*x1;
//OK
A=A1-B1+A2-B2+A3-B3;
//OK
//逆行列
double g11,g12,g13,g21,g22,g23,g31,g32,g33;
g11= (x2*x0-x1*x1)/A; g12=-(x3*x0-x2*x1)/A; g13= (x3*x1-x2*x2)/A;
g21=-(x3*x0-x1*x2)/A; g22= (x4*x0-x2*x2)/A; g23=-(x4*x1-x2*x3)/A;
g31= (x3*x1-x2*x2)/A; g32=-(x4*x1-x3*x2)/A; g33= (x4*x2-x3*x3)/A;
//OK
//最小二乗法
double p[10];
p[0]=g11*x2y+g12*x1y+g13*x0y;
p[1]=g21*x2y+g22*x1y+g23*x0y;
p[2]=g31*x2y+g32*x1y+g33*x0y;
ESTOP0;
}