Other Parts Discussed in Thread: BQ76972, , BQ769142, BQ76942
I want to know how can I calculate the worst-case current measurement error when using any of the BQ769x2 devices (BQ76952, BQ76942, BQ769142, BQ76972).
Can you explain how this is done?
This thread has been locked.
If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.
The accuracy of the current measurement can be conceptualized as the averaging of multiple measurements, then comparing the average against the ideal expected result. This does not consider the noise in a measurement result.
A worst-case error in whole range of the current measurement can be calculated by adding up the individual worst-case offset, gain, DNL and INL errors.
These limits are provided in the datasheet Electrical Characteristics, as seen in Figure-1.
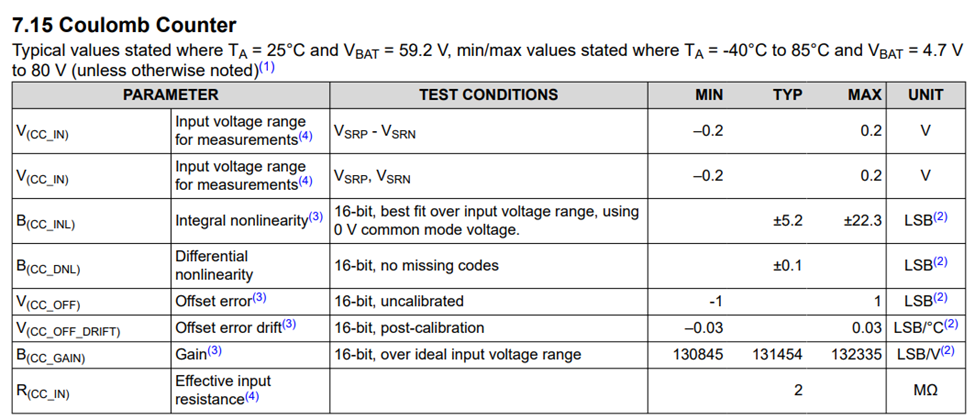
Figure-1. Coulomb Counter datasheet specifications.
All of the limits which affect accuracy are specified in terms of ADC resolution as LSB’s, where. Let’s calculate each individual error:
Adding up all of these factors together, we get a worst-case error of 202.45-LSB. Which would correspond to a voltage of:
![]()
Assuming a 1-mΩ sense resistor, this corresponds to an error of 1.539-mV/1-mΩ = 1.539-A at the 200-mV input (Which would correspond to 200-A of current across 1-mΩ). So, the percentage error would then become 1.539-A/200-A = 0.77%.
Notes: