Other Parts Discussed in Thread: CC1121
Looking for clarity & finality on this subject...
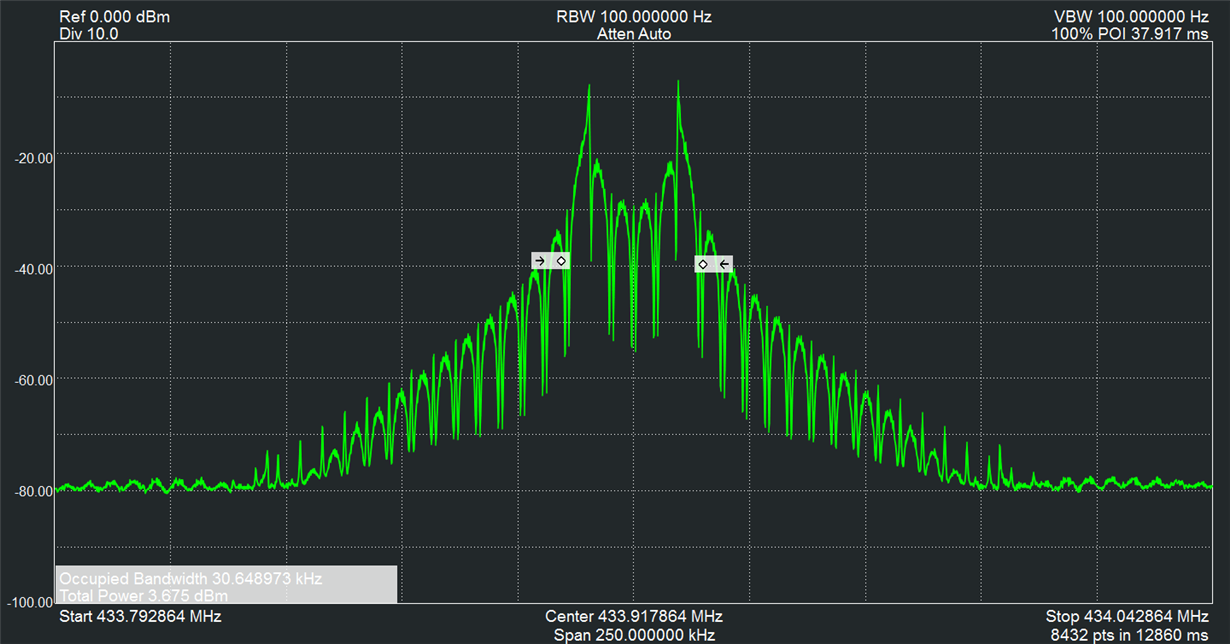
I have seen (5) different iterations on Carlson's Rule for calculating transmitter bandwidth each producing (5) different results.
If dealing with a simple 2-level FSK signal and a simple bit rate, can the formula be simplified or reduced to:
Bandwidth = BPS + Separation
where BPS is 2 x the Modulation Frequency and Separation is 2 x the Frequency Deviation.
So, for a BPS of 4.8KHz and a Separation of 20K, the Bandwidth is 24.8KHz?
(The period of 4.8KBPS being actually 2.4KHz and the Separation being actually the total +/- offset from the CW center frequency.)
Part of the ambiguity that I have seen is Deviation is not always qualified as being strictly a (+/-) figure but sometimes is actually total Deviation (aka Separation).
Thanks,
--
Jay Zebryk