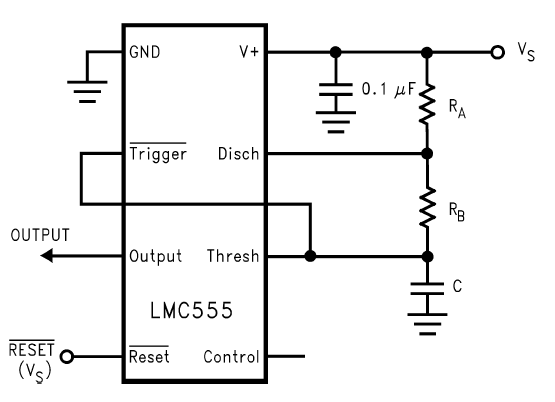
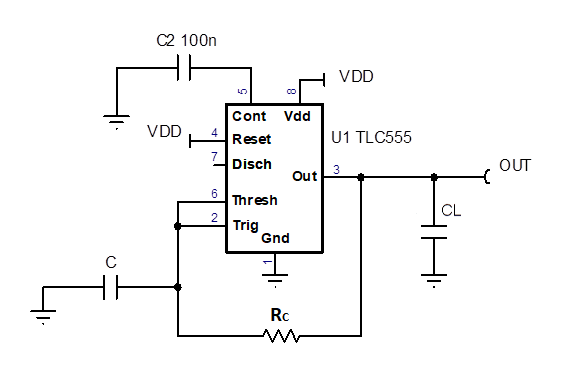
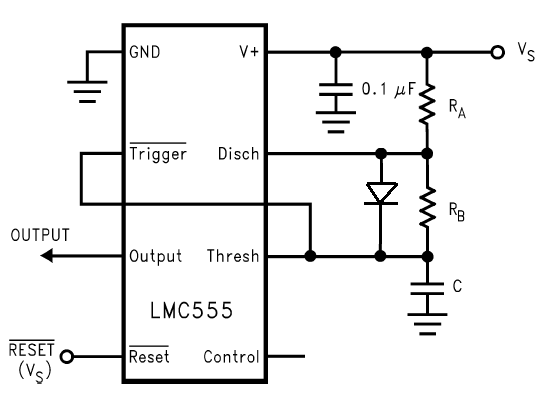
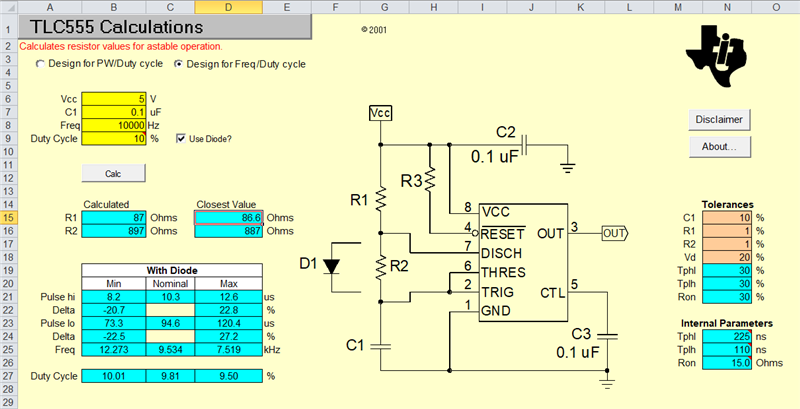
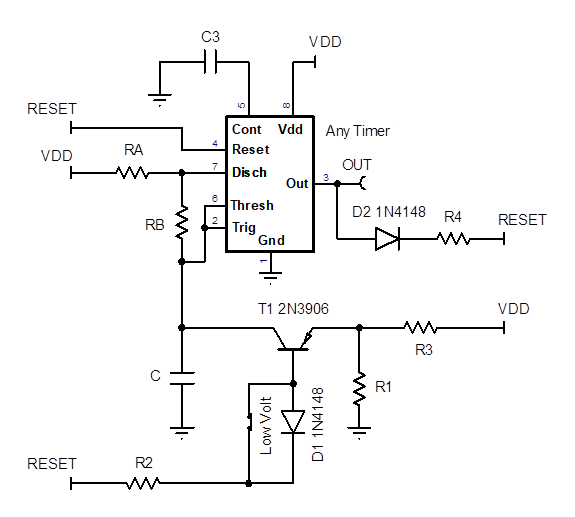
What is the difference between the part numbers?
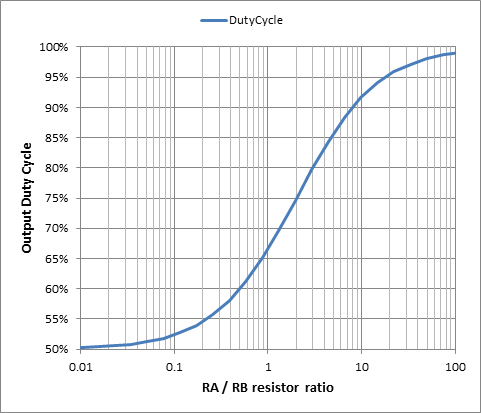
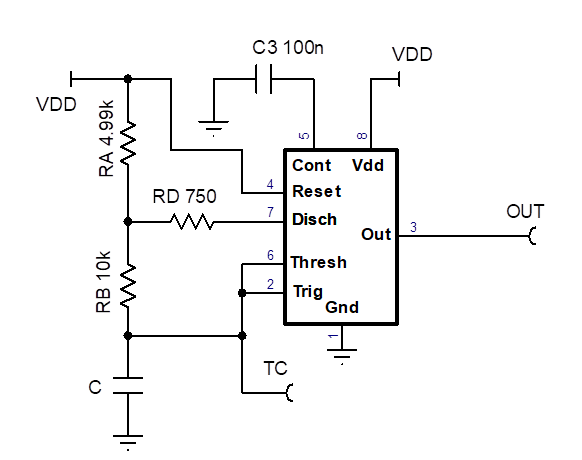
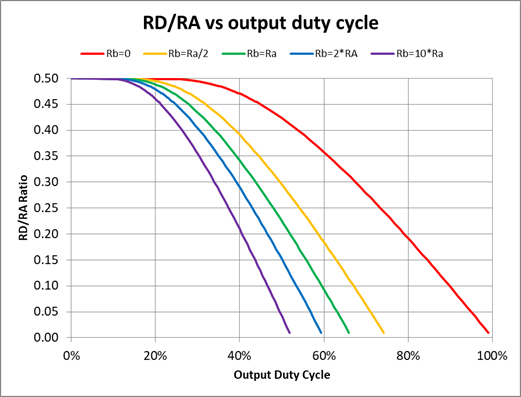
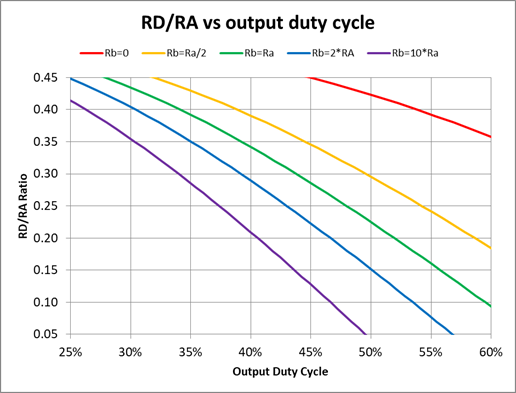
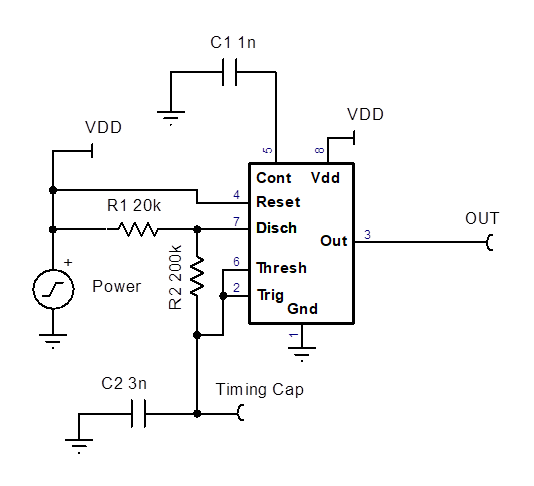
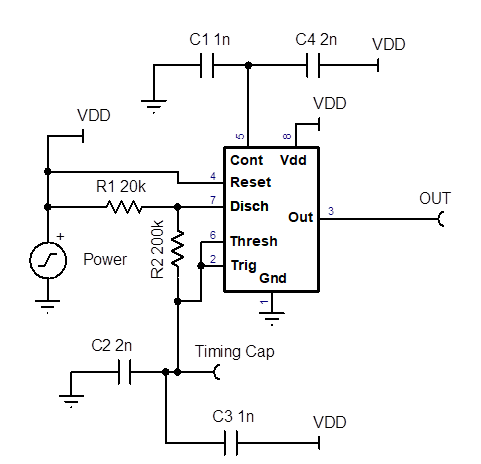
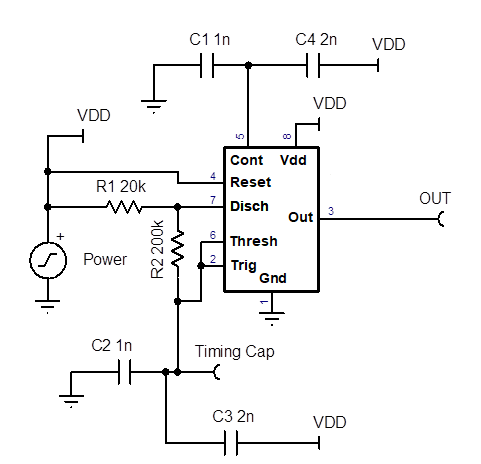
How is the output frequency and duty cycle set?
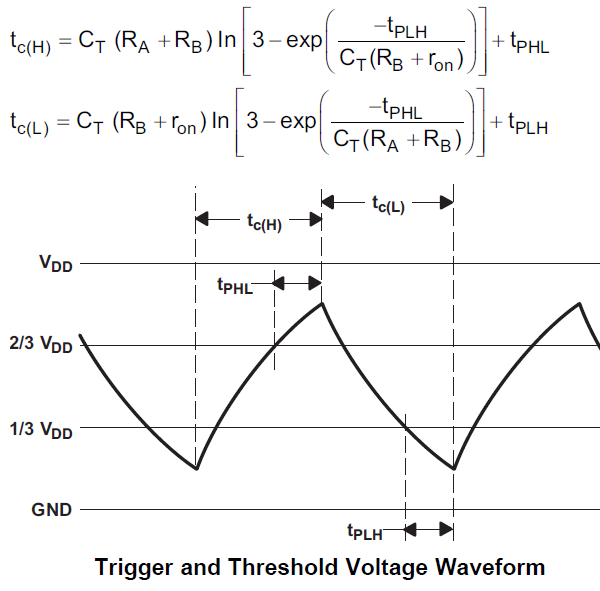
Why is the actual frequency different from the formula, 1.44 / [(RA + 2 * RB) * C] ?
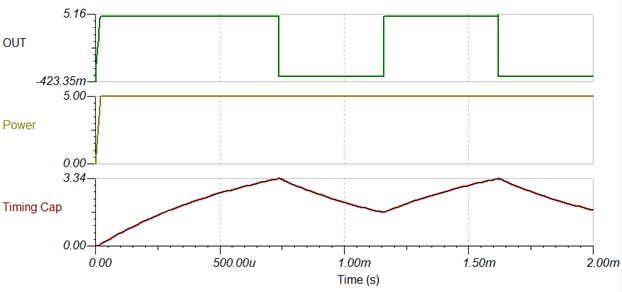
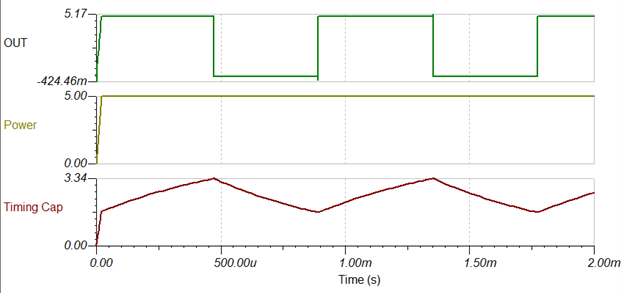
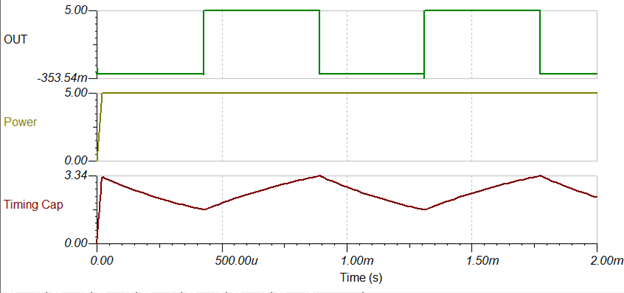
Why is the first output pulse after power up different from the subsequent pulses?
What is the maximum frequency?
What is the minimum frequency?
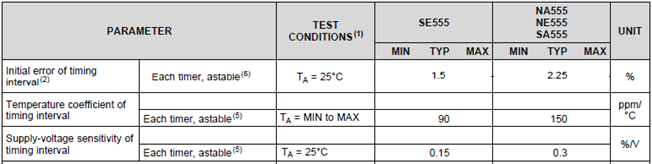
How accurate are the timers?