• State TI Thinks Resolved
  • Locked Locked
  • Replies 2 replies
  • Answers 1 answer
  • Subscribers 50 subscribers
  • Views 257 views
  • Users 0 members are here
Support feedback
Options
Options
Similar topics

This thread has been locked.

If you have a related question, please click the "Ask a related question" button in the top right corner. The newly created question will be automatically linked to this question.

INA226: Measurement resolution and ADC error

Vyshnav vk
Intellectual 440 points
Part Number: INA226
Other Parts Discussed in Thread: INA238, INA228

Dear TI Team,

We are using INA226 in our latest design to measure load Current, Voltage and Power of core supply voltages on the board. So the core supply voltage is 0.8V and max current is 80A. 

We are using a current sense resister of 500uOhm. We would like to know, 

1. Can we increase the sense resistance value?

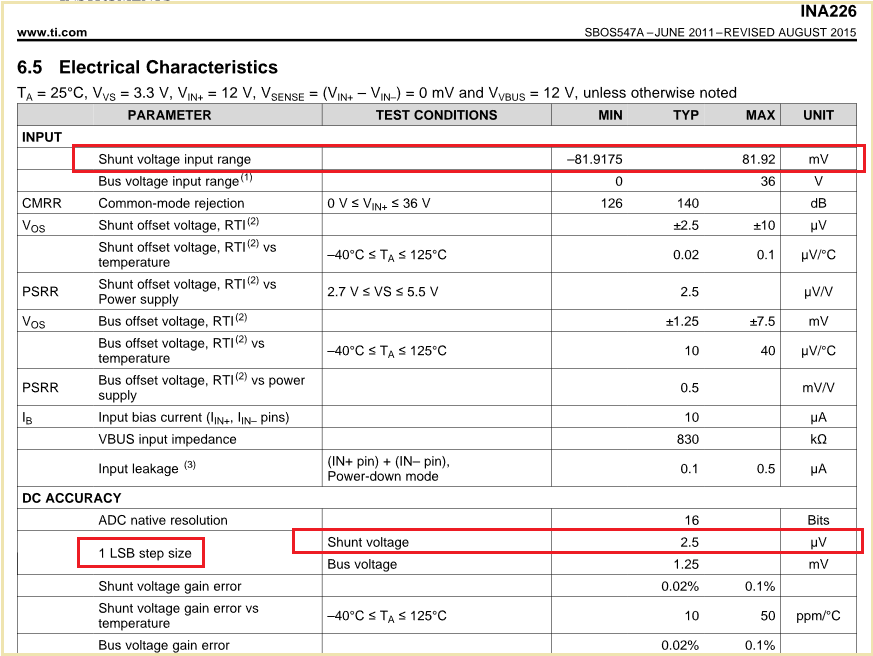
2. What will be the measurement resolution considering the full scale range ( considering ADC error )

3. What is the ADC error and ADC noise which should be considered for design?

4. As per datasheet its 16 bit ADC but we would like to know is there any chance that 1 bit / 2 bit error can happen.?

Kindly provide your input for above queries.

Best Regards,

Vyshnav Krishnan

  • 0
    Guru 140200 points

    Hi Vyshnav,

    this is specified in section 6.5 of datasheet:

    Your voltage drop across the 500µA shunt is 500µA x 80A = 40mV. So, yes, you could increase the shunt resistance.

    But keep in mind that the heat dissipation of shunt will also increase, resulting in 80A^2 x 1mR = 6.4W for a 1mR shunt as an example.

    Kai

  • 0
    TI__Genius 17990 points

    Hello Vyshnav,

    In addition to Kai's comments, we have a video training series that can help you see what how to handle the different error sources: https://training.ti.com/ti-precision-labs-current-sense-amplifiers

    As a side note, you may be interested is using the INA238 (or even the INA228 for even higher accuracy) instead of the INA226.  These newer devices have extra features, and also have a convenient table in the datasheet to help you see the ENOB for accuracy analysis.  Unfortunately, there is no ENOB table for the INA226.

    As for ADC accuracy of the INA226, the device lets you set your conversion time and averaging so that you have some control over accuracy vs noise based on your timing requirements. If you want the highest accuracy, then use the longest conversion time with the highest number of averages.