Hi,
May I know how to check an op-amp is in negative feedback or not.
We used to say when output is connected to inverting terminal of the opamp,it is operating in negative feedback.
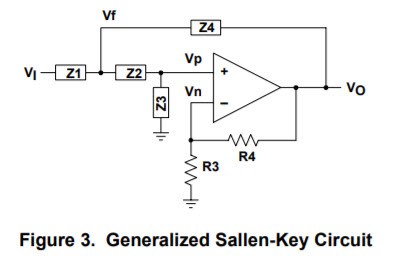
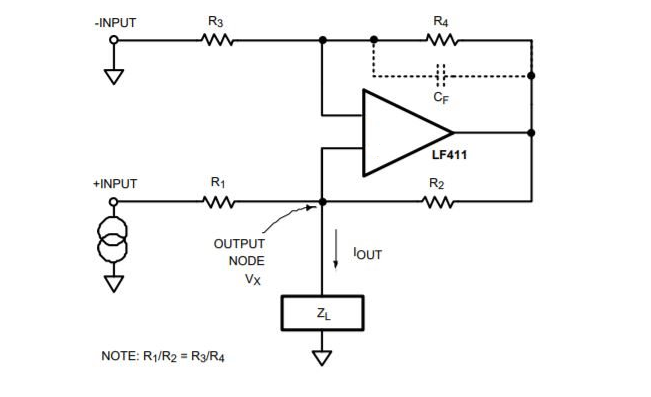
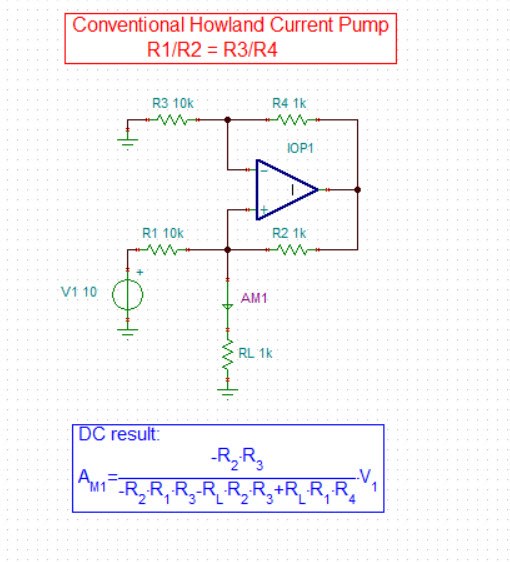
There are many op-amp circuits where output is connected to both inverting and non inverting terminal of the op-amp.May I know in such situations how to check and make sure that
op-amp is operating in negative feedback.
Please see the attached image.
Regards
Hari